volymen av grafen x^2

Phil83762873 skrev:

Hej!

Jobbar med en uppgift där jag ska räkna ut volymen för funktionen y=x^2 upp till linjen y=1, min första tanke var att sätta in 1 i primitiva funktionen men får ut 1/3 vilket låter orimligt då området liknar en halvcirkel och med radien 1 så skulle en halv cirkel haft arean 3.14/2, sedan tänkte jag ta det där ifrån, men det känns fel

jag såg dock en förklaring på internet där volymen kunde direkt räknas ut med  πy^2 dx där x värdet sedan sätts in vid x, men då beräknar de volymen utanför kurvan längs med x axeln och inte volymen innanför funktionen och linjen y=1

några tankar eller tips på hur man bör tänka?

Handlar det om en rotationsvolym? I vilket fall som, börja med att rita upp funktionen, och om det är en rotationskropp även en enkel 3D-skiss.

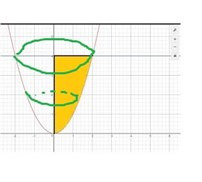
Ja tror det är rotationsvolymen som söks, alltså om ena halvan av kurvan vreds runt y axeln och bildade en skål fast inte ihålig såklart,

se bilden, där den gula arean sedan roterar runt y axeln och bildar en volym, fast där toppen slutar vid y=1 och inte 4 som på bilden,

stämmer det att om man börjar med arean för gula området så måste man ta integralen där x=0 och x=2 och sedan subtrahera den arean från 16 (4x2) för att få gula, eftersom jag hade för mig att integraler räknar ut arean mellan x axeln fram tills det gula området och sedan får man ta bort det från helheten alltså 4x2 för rektangel som bildas

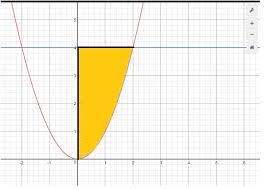
Nej, man behöver räkna ut volymen för varje (väldigt, väldigt tunn) cirkelformad skiva av kroppen och sedan summera dem - när skivornas tjocklek går mot 0 blir detta en integral.