Volymen när en triangel vrids kring y-axel
Lösning:
beräkna volymen av kroppen T som erhålls när den roteras kring y-axeln. T med hörn i (1,1)(1,-1)(2,0)
Man ska ju integrera arean. Den ska ju vridas ett varv så radien borde ju bli 1 på cirkeln om den låg kring origo. Och 2 i detta fall? Gränserna borde bli 1 till 2 på integralen. Hur ska jag få fram formeln som jag ska integrerar, dvs arean. Förstår inte hur man får fram arean här.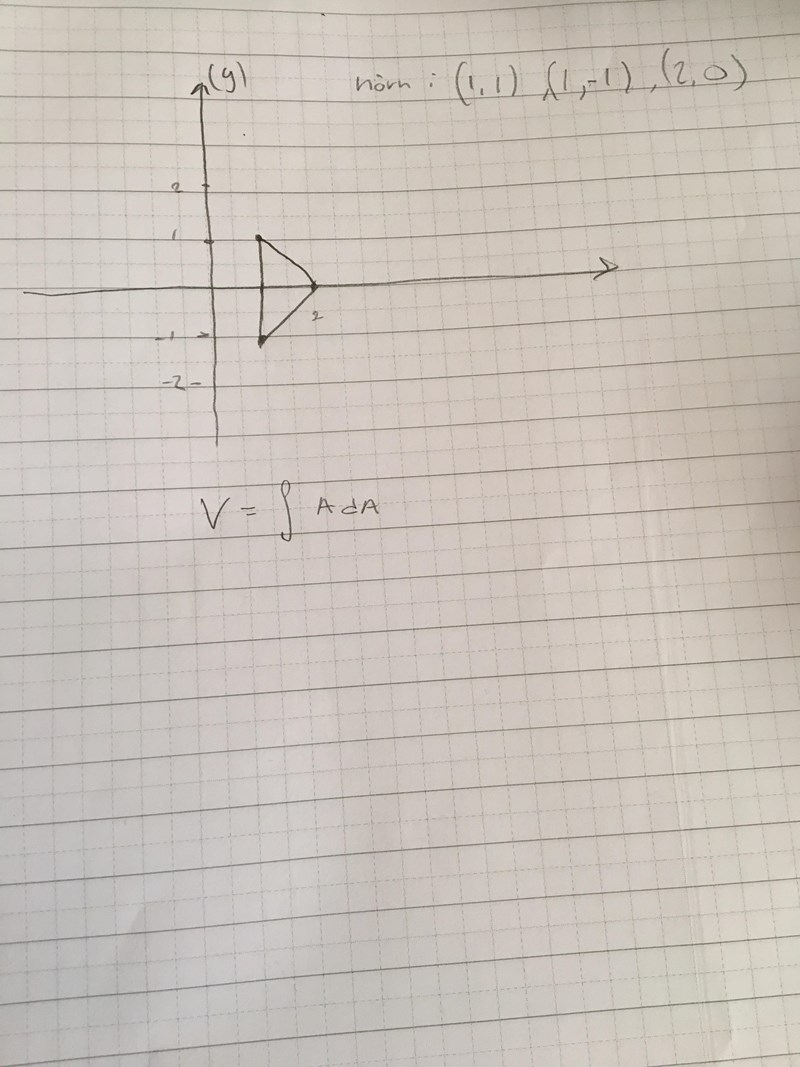
Hur är själva frågan formulerad?
De använder skalmetoden. Känner du till den?
Ett skal på avstånd från y-axeln har omkrets , höjd och tjocklek .
Volymselementet blir därför .
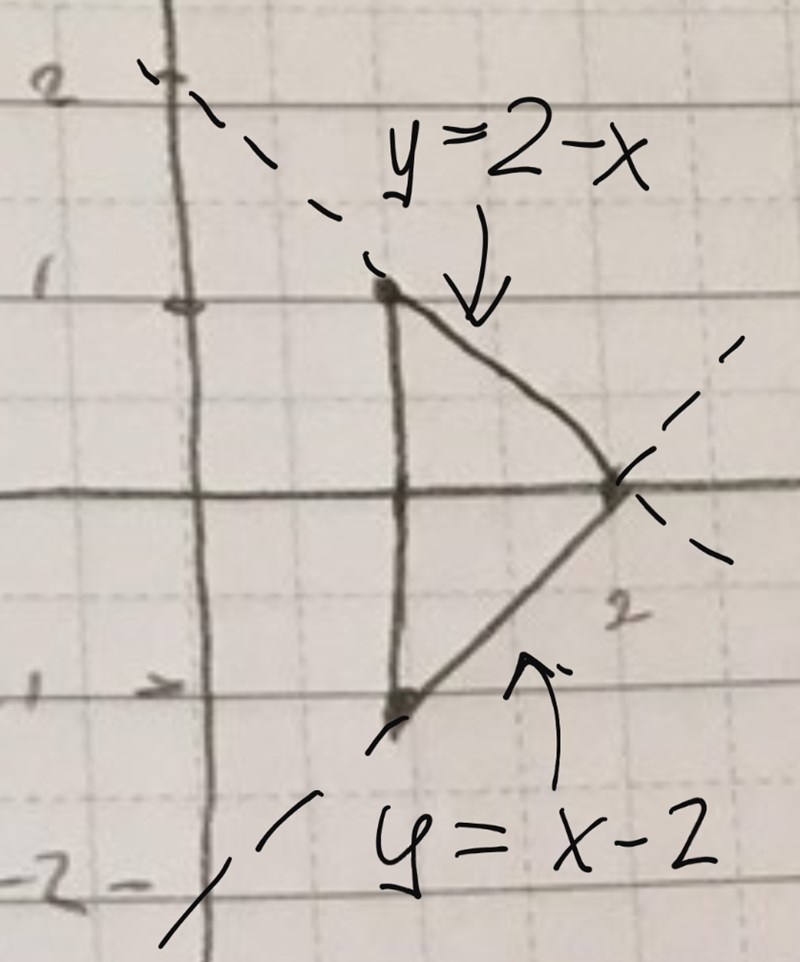
Okej, nej bara skivmetoden, man tänker att höjden är på x-axeln då alltså, 2pix går ju att komma ihåg, men höjden jag lite svårt att förstå hur man kommer fram till. Eller finns det en formel kanske .
Aha tack då tror jag att jag kan lösa detta! Tack så mycket !
Nej det finns ingen formel utan det beror helt och hållet på hur figuren ser ut.
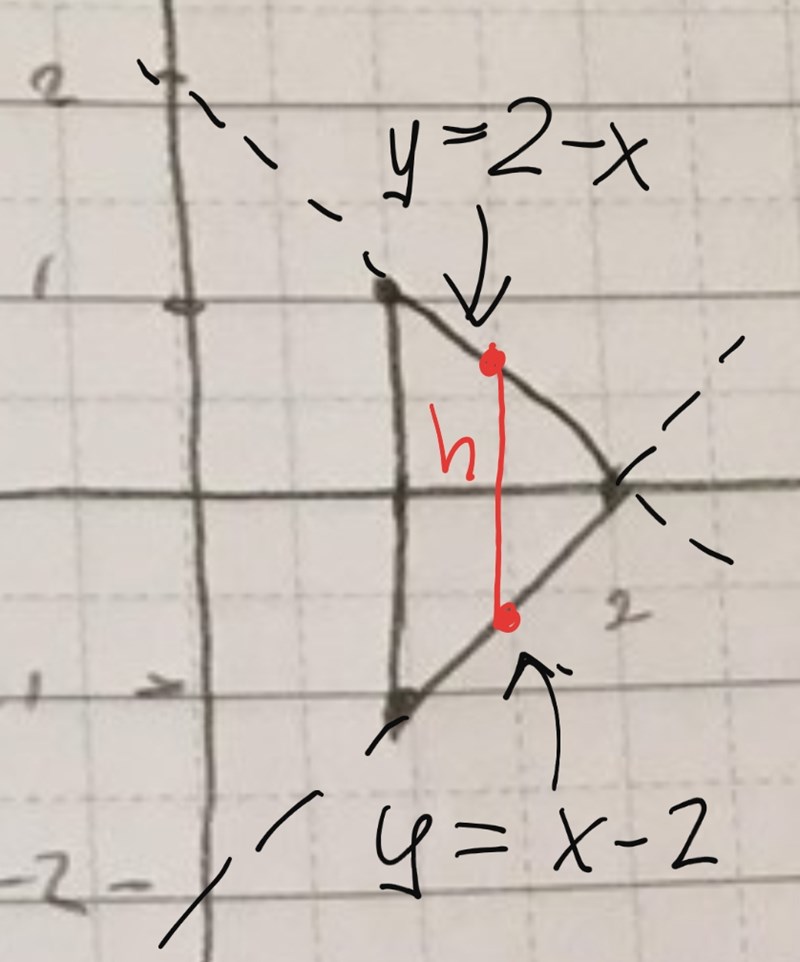
Här ser du att höjden h vid radien x är h = (2-x) - (x-2).
