Vridmoment och cykelpedal
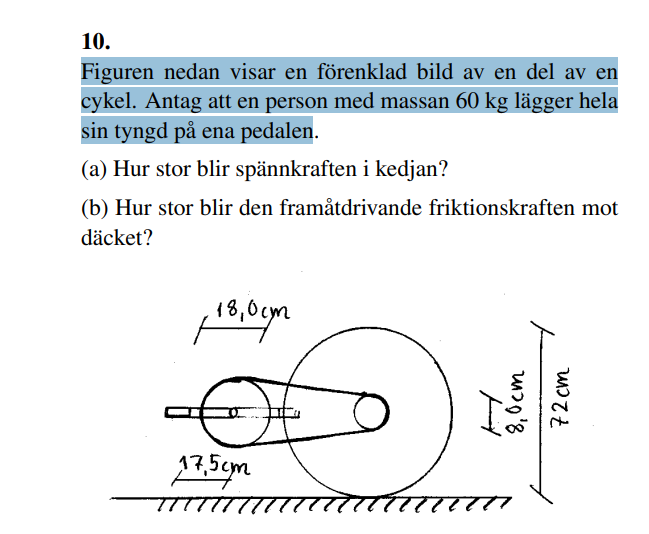
Hej, hittade denna uppgift på nätet men inget facit. Jag vet inte riktigt hur jag ska börja. Jag vet att personen som trampar på pedal utgör en kraft och att kraften i kedjan måste utgöra den andra kraften. Jag försöker sätta upp en kraftekvation där moment medurs = moment moturs men kommer inte så långt. Tänker jag rätt?
JA du är nog inne på rätt tankegång.
Vid pedalen och dess kedjekrans gäller:
Kraften på pedalen gånger pedalaxelns längd är moturs moment.
Kraften i kedjan gånger kedjekransens radie är medurs moment.
För hjulet gäller motsvarande resonemang:
Kraften i kedjan gånger hjulets kedjekrans radie ger moturs moment på hjulet
medurs moment i hjulet fås från friktionkraften och hjulets radie
Alltså, båda frågorna kan lösas med hjälp av kraftmoment? Varför används kedjans radie och inte hela kedjans längd? Vilken motsvarar denna radie?
Kedjans längd spelar ingen roll,
däremot momentarmes längd,
se bild
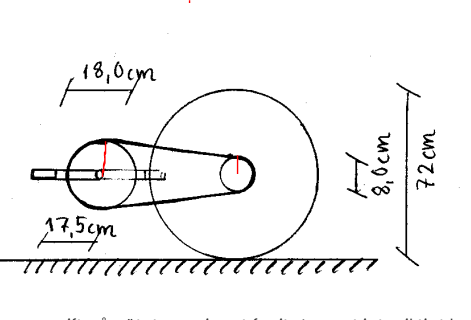
De röda strecken ska visa momentarmarna som kedjan verkar på, det var svårt att rita men de ska vara vinkelräta mot kedjan
Vart är momentpunkten? Du har ritat två olika hävarmar, men verkar dessa på samma momentpunkt?
Det är två olika vridningar med var sin momentpunkt.
Vridningaarna sker runt pedalnavets centrum och runt hjulets centrum.
Alltså vid de röda hävarmarnas underkant.
kan man sedan ställa upp ekvationen: moment medurs = moment moturs om hävarmarna har två olika momentpunkter?
Du får en ekvation för pedalnavets moment
och en annan ekvation för hjulets olika moment.
De två ekvationerna har en variabel gemensamt, kraften i kedjan, som är lika på båda ställena.
Tack!
Hej, jag har löst a uppgiften och hittade facit. Men i b uppgiften står det att friktionskraften är framåtdrivande, varför det? Den bör väl verka åt motsatt håll för att stoppa hjulet från att snurra framåt?
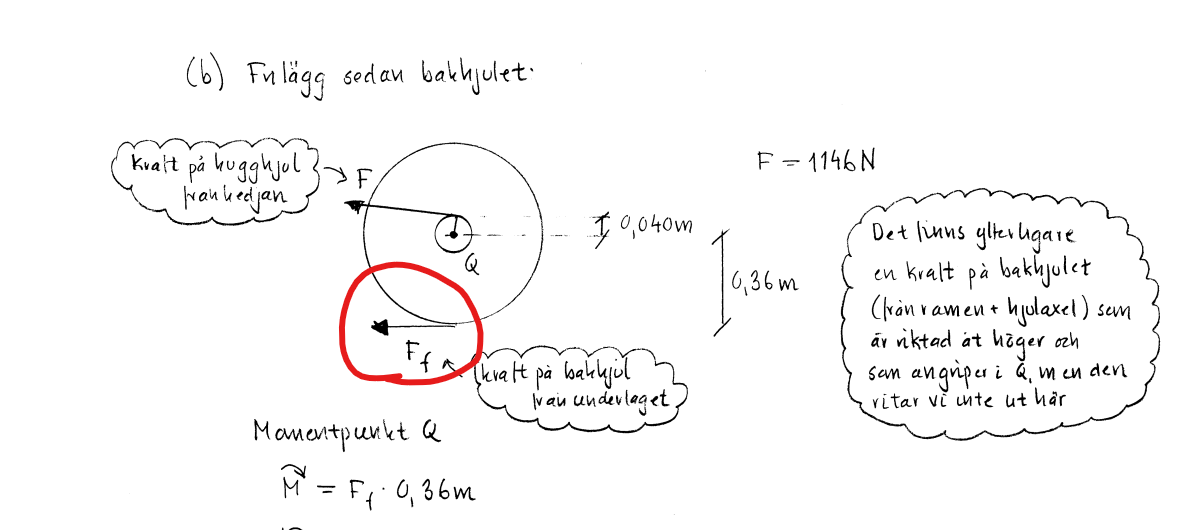
Tänk dig fallet, ingen friktion mellan däck och mark, åt vilket håll kommer däcket att röra sig i kontaktytan mot isen?
Friktionen motverkar den rörelsen.
Rör sig inte hjulet åt vänster? Varför agerar friktionskraften då med rörelseriktningen?
Om det inte finns någon friktion mellan mark och däck kommer hjulet bara att snurra utan att driva framåt.
Friktionen hindrar däcket från att slira mot underlaget, och eftersom däcket rör sig bakåt i kontaktpunkten måste friktionskraften verka framåt.
Det är friktionskraften som gör att cykeln accelererar.
När du bromsar är det tvärtom, då verkar friktionen bakåt.


