What is the positive value of y?

Hej.

Jag har en uppgift som lyder:
If $\frac{b^{x}}{2} = 8 a n d b^{x / 2} = y$ . What is the positive value of y?

Jag rör nog ihop det lite i och med att jag inte vet riktigt hur jag ska separera variabeln b och variabeln x ifrån varandra. Jag hade en tanke om att ta den första ekvationen och multiplicera upp 2:an till 8:an och få b^x = 16. Här kan jag få variabeln b fri genom att upphöja båda led med 1/x. Vi får att b = 16^(1/x). Är jag på rätt väg? Kan jag ersätta mitt värde på b i ekvation 2 för att få ut värde för y?

Du kan nog göra så, men krånglar du inte till det lite då? Ledtråd:

$b^{\frac{x}{2}}=b^{x^(1/2)}$

Det känns som att jag krånglar till det med den metoden som jag bifogade ovan Smutstvätt men vet du vad? Jag tänkte även på det som du tipsade om. Jag blev bara lite kluven kring okända x-värdet i täljaren... Givetvis är det en osynlig 1:a där. Jag ska genomföra uppgiften nu så skickar jag min lösningsmetod strax! 👱🏻‍♀️

Grymt!

Nä men nu hänger jag inte med igen riktigt... Hur menar du när du skriver att: $b^{x / 2}$ kan skrivas om till: $b^{x (1 / 2)}$ Smutstvätt? Jag tappar bort mig lite när jag ser det. Ska jag multiplicera in x:et i bråket? Alltså i både täljare och nämnare?

Prova att logaritmera båda sidorna.

Natascha skrev:
Nä men nu hänger jag inte med igen riktigt... Hur menar du när du skriver att: $b^{x / 2}$ kan skrivas om till: $b^{x (1 / 2)}$ Smutstvätt? Jag tappar bort mig lite när jag ser det. Ska jag multiplicera in x:et i bråket? Alltså i både täljare och nämnare?

Nej. Precis som vanligt är $x\cdot\frac{1}{2}=\frac{x\cdot1}{2}=\frac{x}{2}$ .

Tänker du att jag ska arbeta mig utifrån det här: $l g (b)^{\frac{1}{2} x} = l g (y)$ ? Jag kan skriva om VL till: $(\frac{1}{2} x) l g (b) = l g (y)$

Natascha skrev:
Tänker du att jag ska arbeta mig utifrån det här: $l g (b)^{\frac{1}{2} x} = l g (y)$ ? Jag kan skriva om VL till: $(\frac{1}{2} x) l g (b) = l g (y)$

Ja, och jag tänkte på båda ekvationerna fast jag inte skrev det. Ta den första också.

Så Laguna. Nu har jag gjort vad jag kan för ekvationerna enligt diverse logaritmlagar. 😊

PS: Förlåt för en lite otydlig beräkning och bild överlag... Det brukar vara bättre. 🙈🙈

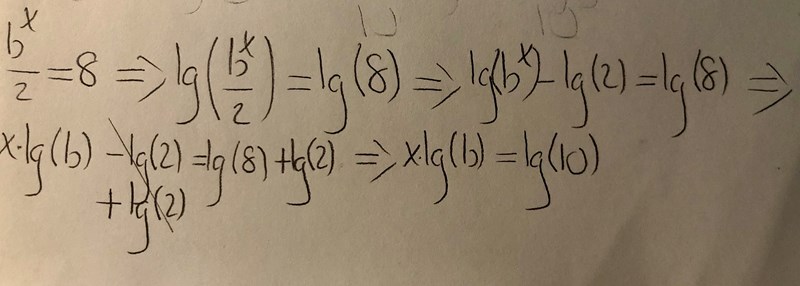
Natascha skrev:
Så Laguna. Nu har jag gjort vad jag kan för ekvationerna enligt diverse logaritmlagar. 😊
PS: Förlåt för en lite otydlig beräkning och bild överlag... Det brukar vara bättre. 🙈🙈

lg(2)+lg(8) är inte lg(10).

Jag är osäker på om mitt förslag egentligen gjorde nånting enklare.

Du krånglar till det något förfärligt. Det behövs inga logaritmer alls.

Visa spoiler

Du vet att

\frac{b^x}{2}=8

så

b^x=16

. Då är

b^{\frac{x}{2}}=16^{\frac{1}{2}}=\sqrt{16}=4

Smaragdalena, jag kan ej se vad du skrivit i din "Spolier". :( Jag tycker också att det ser väldigt konstigt ut alltihopa men kan vi ta det stegvis med din metod då?

Nu bör formlerna i spoilern fungera. Jag hade skrivit lite fel och glömt att kolla att den fungerade. Titta igen!

(En moderator som inte kan logga in checkar in för kvällen)

Det var Smaragdalenas lösning som jag tänkte på, men det blev väldigt ful latex. :)

(För den som ur Pluggakuten förbannats, är mobilen ett verktyg ändå)

Tack Smaragdalena för ditt svar. Jag kom igång med den metoden du tog upp ovan i början. Jag fick ut att b^x = 16. Sedan visste jag inte riktigt vart jag skulle ta vägen. Jag hade även lite svårt hur och var jag kan ersätta värdet 16 i ekvationen: $b^{\frac{x}{2}} = y$ . Jag kom efter en stund fram till att den ekvationen är förenklad från: $b^{x (1 / 2)} = y$ . Då lossnade allt och jag såg tydligt att b^x ersätts av 16^(1/2) som är detsamma som sqrt(16) = 4. :)

Jag skulle löst den enligt följande:

$y=b^{x/2}=\sqrt{b^x}=\sqrt{\frac{2b^x}{2}}=$

$\sqrt{2}\cdot \sqrt{\frac{b^x}{2}}=\sqrt{2}\cdot \sqrt{8}=$

$\sqrt{16}=4$

Svara Avbryt

Visa senaste svar