z4= w
ekvationen z^4 = w har en lösning z1 = 1+i
vilka är de andra lösningarna?
alltså jag vet att z1 har roten ur två( cos45+isin45) och dess konjugat måste vara z2= roten ur (-45+180)+isin(-45+180) , sen kommer jag ej på de andra lösningarna..
Rita ut lösningen i det komplexa talplanet.
De andra lösningarna har samma belopp och skillnaden i argument mellan två närbelägna lösningar är ett fjärdedels varv.
okej jag ritade ut den. Nu är frågan vad deras vinklar är och jag vet ej hur man kan se det?
Har du verkligen ritat:
+1+ i
+1- i
-1+ i
-1 - i
...åsså ser du inte vinklarna?
Jo då. Men jag kom på ett annat sätt nu, man kan utveckla paretensen upphöjt till 4 så blir 4i^2 vilket blir - 4
z^4 = - 4 och så kan man lösa ekvationen för att komma fram till samtliga 4 rötter. Tack ändå!
sen kan man se i enhetscirkeln att de ligger på första , andra och tredje etc.
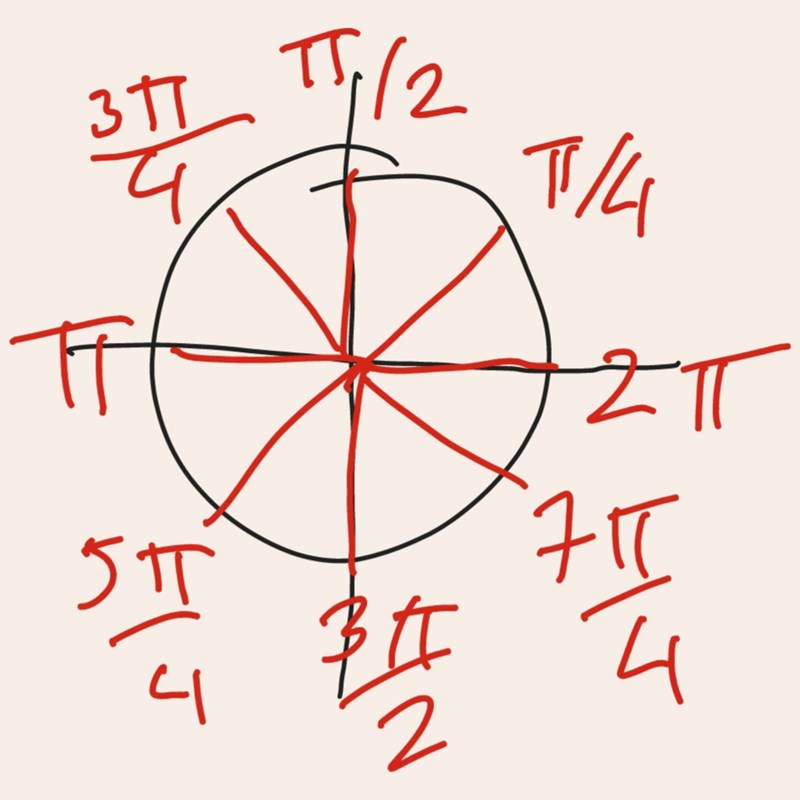
Du behöver lära dig att känna igen alla multiplar av (d v s alla multiplar av 45o) när de är ritade på rutat papper.
Hur menar du att känna alla multiplar av 45 ?
Om 45 grader ligger på första kvadranten , så vet man att -45 ligger i fjärde kvadranten
Mahiya99 skrev:Hur menar du att känna alla multiplar av 45 ?
Så här: