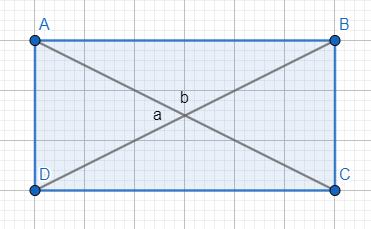
2016 Q29
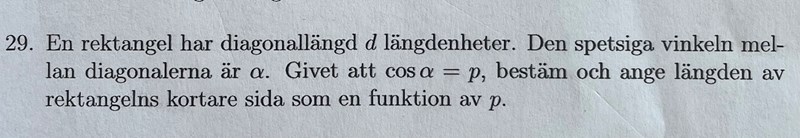
 Såhär tänker jag men det stämmer inte med facit
Såhär tänker jag men det stämmer inte med facit
Var gör jag för fel?
Du ritade en triangel. Rita en rektangel med diagonalerna istället.
Macilaci skrev:Du ritade en triangel. Rita en rektangel med diagonalerna istället.
Men blir inte en rektangels diagonal en triangels hypotenusa? Ritade en triangel då jag tänkte att de va endast detta av rektangeln som spelade roll
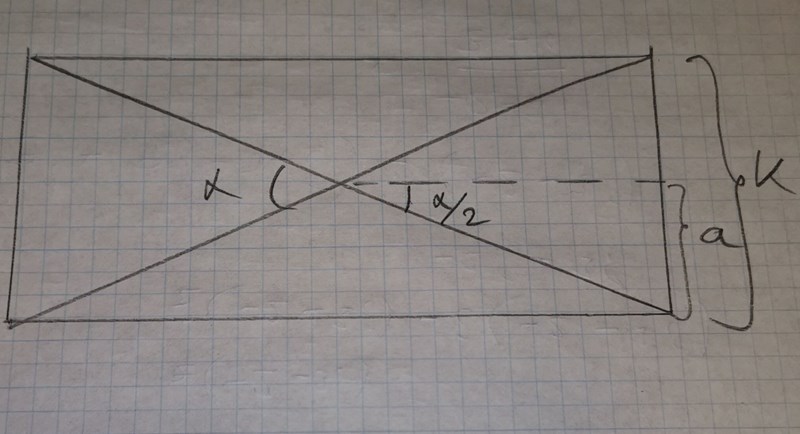
Läs frågan en gång till: Den spetsiga vinkeln mellan diagonalerna är α. Du har valt fel alfa.
rapidos skrev:Läs frågan en gång till: Den spetsiga vinkeln mellan diagonalerna är α. Du har valt fel alfa.
vilket är alpha: a eller b? Hur man bestämmer?
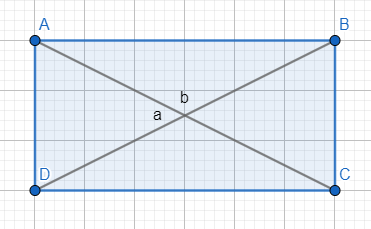
https://www.pluggakuten.se/trad/mafy-2016-uppgift-29/
Mahiya99 skrev:https://www.pluggakuten.se/trad/mafy-2016-uppgift-29/
Varför a? Både a och b är spetsiga här.
Elev01 skrev:Mahiya99 skrev:https://www.pluggakuten.se/trad/mafy-2016-uppgift-29/
Varför a? Både a och b är spetsiga här.
Tror man ska tänka att de är likbenta.
Ok jag förstår nu det är a eftersom a+b=180 och a>b. a<90 och b>90
Elev01 skrev:rapidos skrev:Läs frågan en gång till: Den spetsiga vinkeln mellan diagonalerna är α. Du har valt fel alfa.
vilket är alpha: a eller b? Hur man bestämmer?
Vinkeln b är trubbig.
Jag visade uppgiften för någon på en räknestuga och han säger cosinussatsen för att få sidan b och sedan Pythagoras sats för att räkna ut kortare sida
Elev01 skrev:
Gjorde fel.. Skickar en ny bild
Alternativ lösning med hjälp av formeln för halva vinkeln
eftersom cos(alfa) = p får vi
samtidigt vet vi att sinus(x) = (motstående katet)/hypotenusa
Motstående katet = a, eller k/2 enligt figuren och hypotenusan är d/2
alltså gäller sin(alfa/2) = k/d
vilken kan förenklas(?) till
Oj jag måste verkligen ha läst för snabbt :) då blev det mycket mer förståeligt