2021 fråga 14
 Hej, jag undrar hur man löser fråga 14.
Hej, jag undrar hur man löser fråga 14.
Rätt svar är:
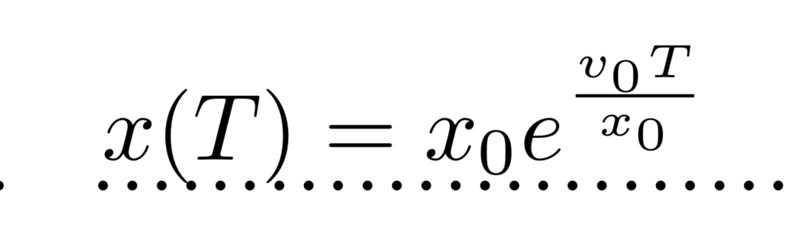
Hur kommer e in i bilden? Blir det någon diffekvation?
Vi har en funktion (x) vars derivata (v) är proportionellt mot själva funktionen. Ja, vi har en diffekvation.
Yes det är en diffekvation.
x är en funktion som varierar med t, dvs x(t), v är tidsderivatan av x, dvs x'(t). Tänk på at x0 och v0 är konstanter.
Flytta över allt till vänsterled så får du:
, som har lösningen .
Mha begynnelsevillkoret x(0)=x0 får du C = x0, pluggar du sedan in t=T får du det sökta resultatet.
Ah tack, förstår nu! Måste varit första diffekvationem på mafy
Låter bra.
Har funnits ett par angående fjädrar innan som kan lösas mha diffekvationer (andra ordningens i dessa fall), men måste hålla med om att man blir "lurad" av att de inte skriver ut x(t) i högerled, utan bara x. Det blir inte självklart att det är en diffekvation som ska lösas.
fågelskit skrev:Det blir inte självklart att det är en diffekvation som ska lösas.
Om man tittar ser man .
Jo det är klart att det är det som står, menade bara att för den stressade provskrivaren blir det lätt att tolka x som den oberoende variabeln, när det egentligen är t. Menade dvs inte att frågan är missvisande, dåligt formulerat av mig.
Varför
Varför måste man subtrahera ?


