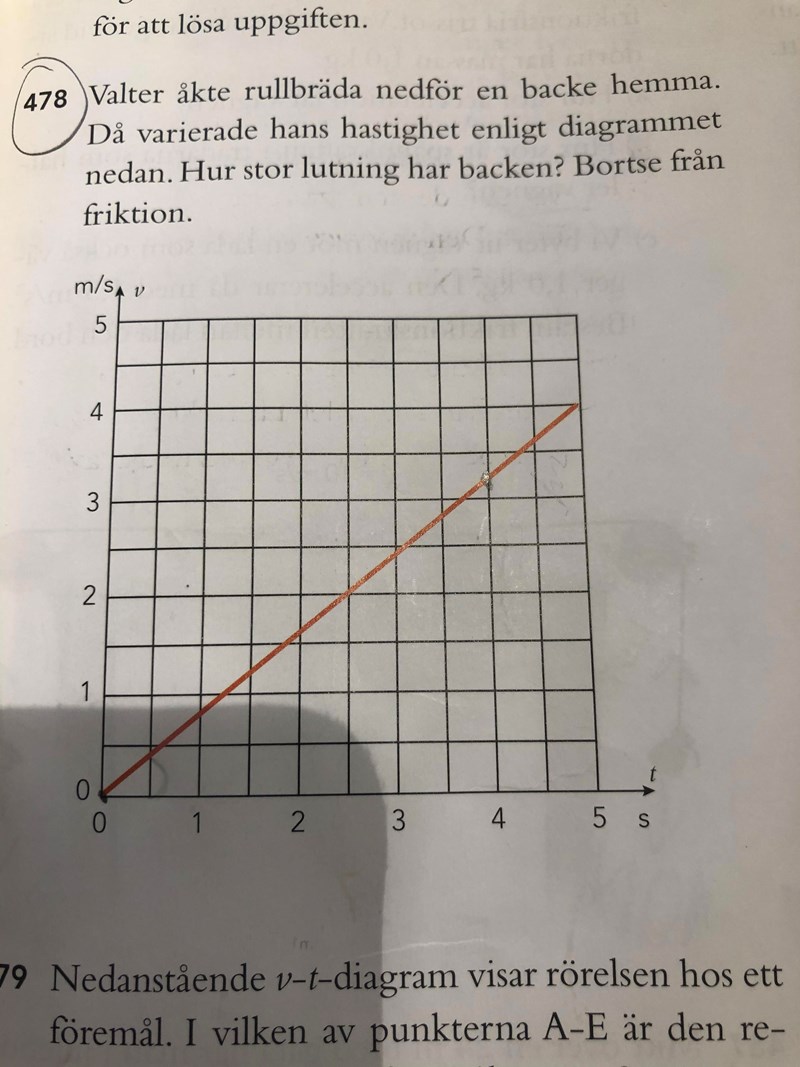
478
 Hur ska man tänka? Vad är felet med min uträkning?
Hur ska man tänka? Vad är felet med min uträkning?
För att lösa uppgiften vill man använda sig av formeln för Newtons andra lag, samt försöka stryka bort de termer man inte har tillräckligt med information för att beräkna, så som du själv försökt göra med "mg". Samtidigt bör man först lista ut Valters acceleration, samt även använda hans tyngdacceleration (9,82 m/s^2) när du beräknar backens lutning. I slutändan är det tangens som funkar bäst i just denna uträkning. Lycka till!
(Nedanför kan du se hur du löser uppgiften)
Det första man vill beräkna är i alla fall grafens lutning (Valters acceleration). Valters acceleration kan man beräkna genom att skriva ner två koordinater från grafens linje och sedan använda sig av formeln (y2-y1)/(x2-x1) för att beräkna dess k-värde (lutning). Detta beror på att y-axeln beskriver Valters ökning i m/s (hastighet), samtidigt som x-axeln beskriver ökningen i tid (sekunder). Grafens lutning (k-värdet) beskriver därför Valters ökning i hastighet per sekund, med andra ord accelerationen:
Det andra värdet man behöver är Valters tyngdacceleration, vilket är 9,82 m/s^2, något som inte kräver en uträkning för att konstatera. Efter att man skrivit ner dessa värden kan man gå vidare till att rita ut ett lutande plan:
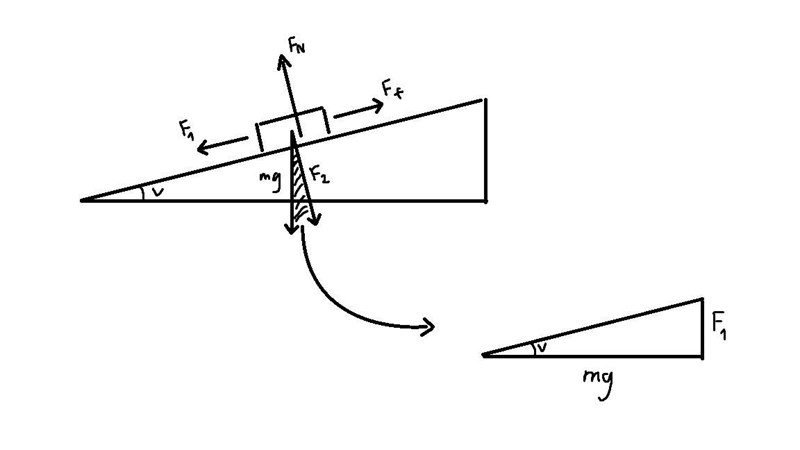
Den hänvisade vinkelräta triangeln är den form vi vill arbeta med. Själva uppgiften är att ta reda på vad vägens lutning är, vilket översätt till vårt sammanhang kan formuleras som "hur många grader är vinkeln v?". Vanligtvis finns det ett antal trigonometriska sätt att lösa detta på: exempelvis kan man använda sig av inversen på tangens, sinus eller cosinus. I uppgiften får man däremot inte tillräkligt mycket information för att lösa ut "v" på något annat sätt än med tangens. Det man vill göra är därför att lösa ut kraftresultanten F1:
Det näst sista steget i uträkningen är att finna en formel som man kan sätta in alla värden man har beräknat. Denna formel beskrivs av newtons andra lag, och är: Fr = m * a. Det man vill göra är att sätta in F1 som den okända kraftresultanten i "Fr". Därefter vill man ersätta "a" med hastigheten 0,8, och i slutändan ersätta "g" med tyngdaccelerationen 9,82. Gör man detta borde man få det följande resultatet:
Ovanför kan man se hur termen "m" vistas på båda sidan av leden. Dividerar man bort "m" på det ena ledet divideras konsekvent "m" ur det andra. Av denna anledningen stryks termen bort. Det som man har kvar borde nu vara:
Det sista steget i uträkningen är att lösa för tan(v). Detta kan man göra genom att dividera 9,82 på båda leden, så att tan(v) blir ensam på vänster sida. Därefter använder man sig av inversen på uttrycket för att beräkna hur många grader "v" är.
I slutändan kan man därför konstatera att backens lutning låg på 4,7 grader.

