Absolutbelopp, är detta rätt? (Matematik/Matte 3/Trigonometri)

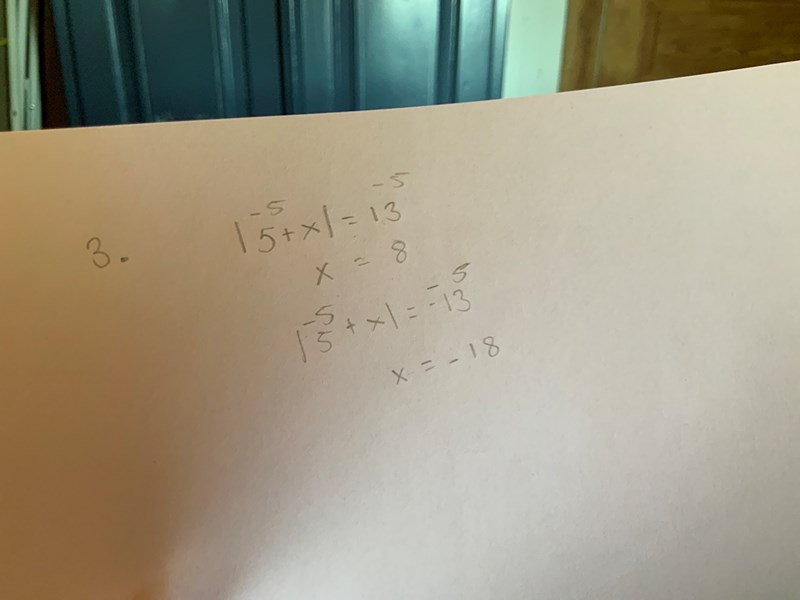
Jag hade ritat upp en tallinje så här typ.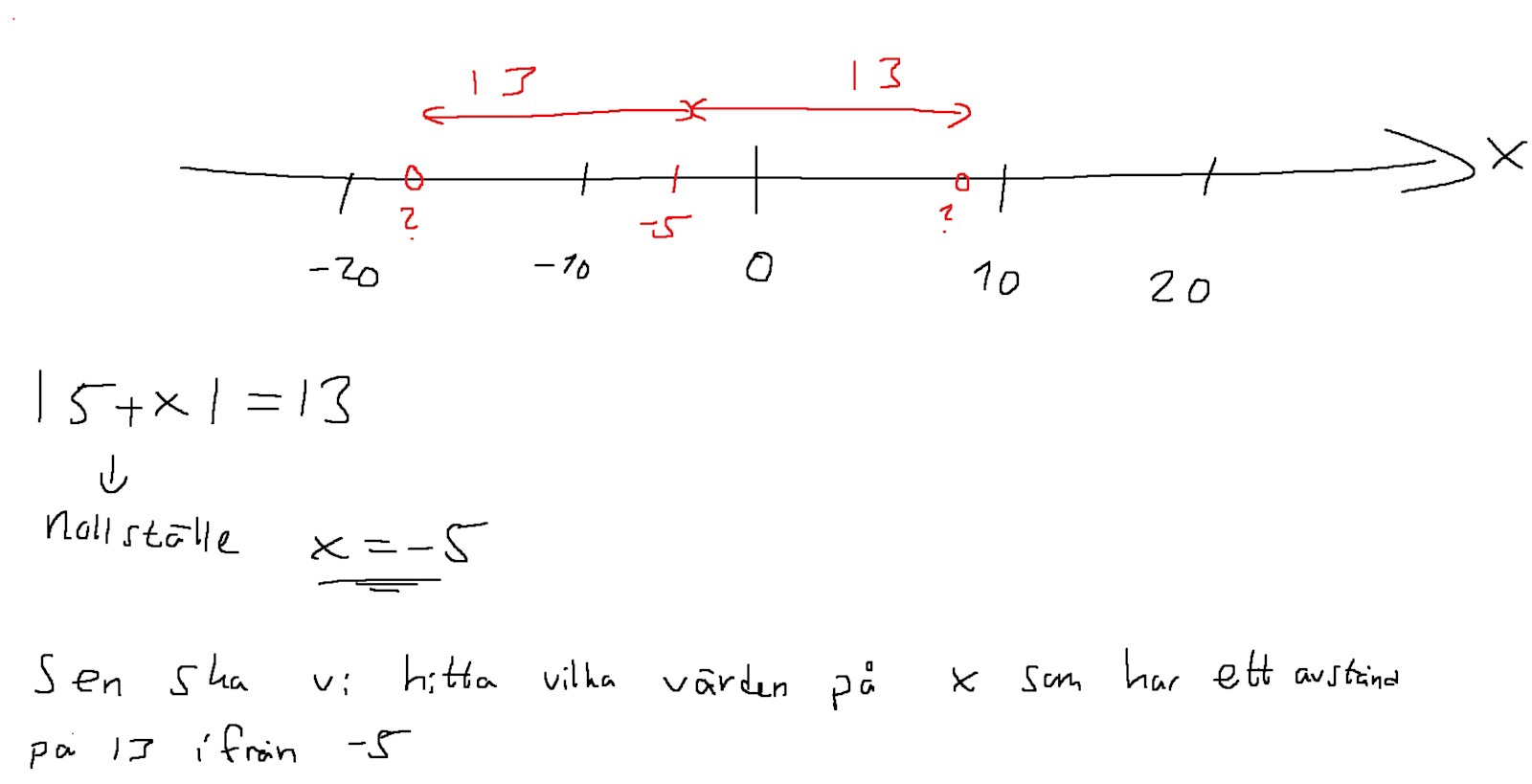

Det ser ut som att du har hittat en av lösningarna, men det finns en till!

Egocarpo skrev:
Jag hade ritat upp en tallinje så här typ.

Det ser ut som att du har hittat en av lösningarna, men det finns en till!

Vilken är en av lösningarna och hur skulle man lösa den uppgiften utan tallinje?

Du hittade ju -18. Du kan alltid testa om du har hittat en lösning genom att stoppa in.

Vi tror x=-18 löser ekvationen.

|-18+5|=|-13|=13 Ok uppfyller ekvationen.

Du hittade x:et som ger -13 inuti absolutbeloppet, kan du hitta x:et som ger 13 inuti absolutbeloppet?

sofiakatarina skrev:
... hur skulle man lösa den uppgiften utan taltallinje

Du kan lösa den utan tallinje på två olika sätt.

1. Grafiskt

Rita grafen till y = |5+x|
Rita grafen till y = 13
Hitta grafernas skärningpunkter.
Lösningen utgörs av dessa skärningspunkters x-koordinater.

2 Algebraiskt:

Dela upp ekvationen i de två delarna $x<>$ och $x\geq -5$ .
Skriv om ekvationen i dessa två intervall, där du utnyttjar att $|5+x|=-(5+x)$ då $x<>$ och $|5+x|=5+x$ då $x\geq -5$
Lös ekvationerna och kontrollera att lösningarna hamnar inom de tillåtna intervallen.

För att lösa den här typen av enkla absolutvärdesekvationer finns det ett rätt enkelt sätt. Man kan använda sig av följande definition: $\sqrt{x^{2}} = |x|$ och gå baklänges.

Lösning

|5 + x| = 13 \sqrt{{(5 + x)}^{2}} = 13 {(5 + x)}^{2} = 169 5 + x = \pm 13 x_{1} = 8, x_{2} = - 18

naytte skrev:
För att lösa den här typen av enkla absolutvärdesekvationer finns det ett rätt enkelt sätt. Man kan använda sig av följande definition: $\sqrt{x^{2}} = |x|$ och gå baklänges.

Lösning
$|5 + x| = 13 \sqrt{{(5 + x)}^{2}} = 13 {(5 + x)}^{2} = 169 5 + x = \pm 13 x_{1} = 8, x_{2} = - 18$

jag fick ju de svaren utan att gå den vägen... kolla min bild.

sofiakatarina skrev:
naytte skrev:
För att lösa den här typen av enkla absolutvärdesekvationer finns det ett rätt enkelt sätt. Man kan använda sig av följande definition: $\sqrt{x^{2}} = |x|$ och gå baklänges.

Lösning
$|5 + x| = 13 \sqrt{{(5 + x)}^{2}} = 13 {(5 + x)}^{2} = 169 5 + x = \pm 13 x_{1} = 8, x_{2} = - 18$

jag fick ju de svaren utan att gå den vägen... kolla min bild.

Mitt sätt är bättre eftersom det fungerar i alla situationer. Du har ju inte visat hur du har tänkt i din.

Du verkar ha tänkt rätt från början, men missat att skriva hur du tänkte.

Om absolutbeloppet av ett uttryck är 13 så är uttrycket antingen lika med 13 (första fallet) eller lika med-13 (andra fallet)

Du har löst de två fallen, men utan att berätta varför du löste dem.

Dessutom skrev du i första fallet ett beloppstecken som inte bör vara där, och i andra fallet ett beloppstecken som är fel. Beloppet är inte -13.

Bubo skrev:
Du verkar ha tänkt rätt från början, men missat att skriva hur du tänkte.

Om absolutbeloppet av ett uttryck är 13 så är uttrycket antingen lika med 13 (första fallet) eller lika med-13 (andra fallet)

Du har löst de två fallen, men utan att berätta varför du löste dem.

Dessutom skrev du i första fallet ett beloppstecken som inte bör vara där, och i andra fallet ett beloppstecken som är fel. Beloppet är inte -13.

Hur ska jag göra det då?

Man kan också öva på att översätta ekvationer till "gåtor".

|5 + x| = 13 är samma sak som |x + 5| = 13
VL anger [avståndet från x till -5] HL är 13 rakt av.

Gåtan blir:
För vilka värden på x är det sant att
[avståndet från x till -5] är lika med 13?

Med "avstånd" menar vi avstånd längs tallinjen.
Se Egocarpos figur!

sofiakatarina skrev:

Hur ska jag göra det då?

I det här fallet, när det endast finns ett uttryck med absolutbelopp, kan du göra på följande sätt:

|5+x| = 13

Det finns två fall:

5+x = 13, villet innebär att x = 13-5 = 8.
5+x = -13, vilket innebär att x = -13-5 = -18.

Yngve skrev:
sofiakatarina skrev:

Hur ska jag göra det då?

I det här fallet, när det endast finns ett uttryck med absolutbelopp, kan du göra på följande sätt:

|5+x| = 13

Det finns två fall:

5+x = 13, villet innebär att x = 13-5 = 8.

5+x = -13, vilket innebär att x = -13-5 = -18.

hur ska jag visa hur jag tänker...

naytte skrev:
För att lösa den här typen av enkla absolutvärdesekvationer finns det ett rätt enkelt sätt. Man kan använda sig av följande definition: $\sqrt{x^{2}} = |x|$ och gå baklänges.

Lösning
$|5 + x| = 13 \sqrt{{(5 + x)}^{2}} = 13 {(5 + x)}^{2} = 169 5 + x = \pm 13 x_{1} = 8, x_{2} = - 18$

kan du visa steg för steg hur du löste denna ekvation.. för förstår inte hur du gick tillväga här

sofiakatarina skrev:

hur ska jag visa hur jag tänker...

Det beror på. Hur tänker du?

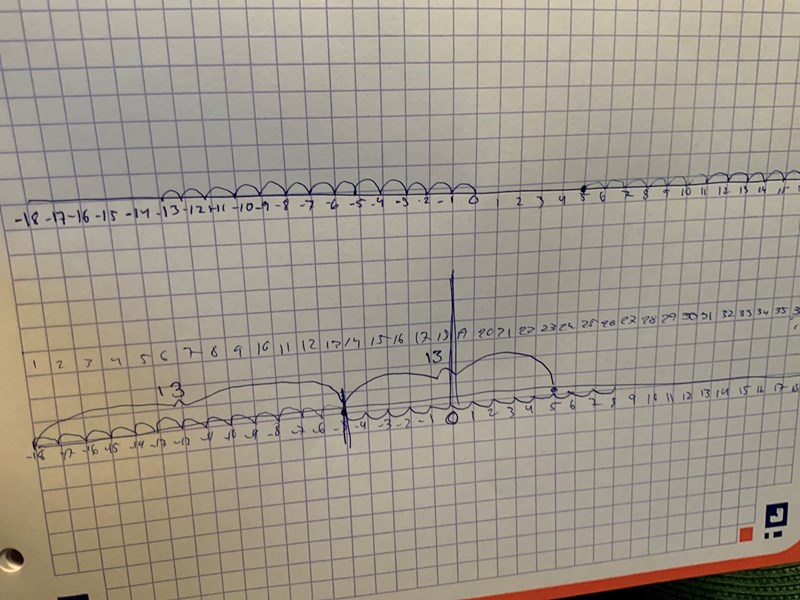vänta vänta jag fattar.. man utgår från -5 och om man sätter ut det på en tallinje så blir det så att går man 13 steg åt båda hållen så blir det för mig 13 steg åt vänster från -5 alltså -18 och 13steg och höger från -5 alltså 8...

men vad betyder -5.. att det är ett nollställe?

sofiakatarina skrev:
vänta vänta jag fattar.. man utgår från -5 och om man sätter ut det på en tallinje så blir det så att går man 13 steg åt båda hållen så blir det för mig 13 steg åt vänster från -5 alltså -18 och 13steg och höger från -5 alltså 8...

Ja det stämmer.

men vad betyder -5.. att det är ett nollställe?

Man kan se uttrycket |x-a| som avståndet mellan talet x och talet a. Alltså är |x+5| = |x-(-5)| lika med avståndet mellan talet x och talet -5.

Se inlägg #11