Vart är felet? Procent

Mellan 2003 och 2004 var det ingen förändring, andelen förblev lika stor. Hjälper det? 

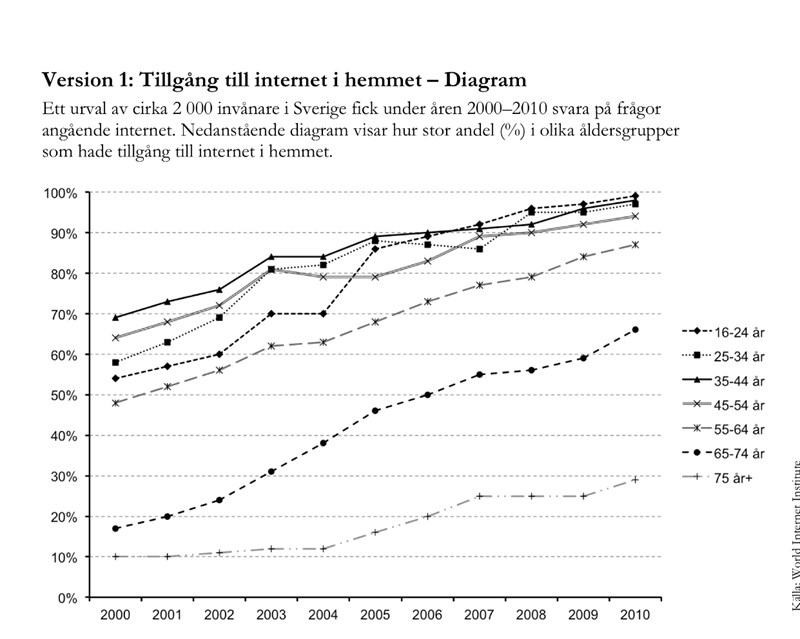
Jag vet inte vad du får förändringsfaktorerna ifrån. Jag gissar att du försöker läsa av de från grafen år för år. Det går inte riktigt att göra. Diagrammet har en skala så att man inte kan utläsa exakt hur många det är varje år men det behöver du inte. De är intresserad av hur mycket det ökat med under perioden 2000 till 2010. Då räcker det att titta på det första och sista året och jämföra.

Då kan du se att 2000 är det ungefär 10 procentenheter och 2010 så är det ungefär 30 procenenheter.

Du kan nu titta hur mycket procentuellt det har ökat.

Antingen genom att ta$\frac{ökningen(/skil\ln aden)}{det ursprungliga}$= 

Då får du ut den procentuell ökningen eller

$\frac{nya värdet}{gamla värdet}$ då får du fram förändringsfaktorn.      

Det du gör skulle kunna bli rätt om det gick att läsa av ökningen exakt rätt för varje år. Men diagrammet har för låg upplösning, så du får små fel i varje avläsning. Sedan multipliceras felen och du får fel värde.

Gör i stället så här: Läs av andelen år 2000 och andelen 2010 och beräkna ökningen direkt i stället. Du behöver inte mellanvärdena!

Så jag ska ta  (30%-10%)/10 = 2 = 200%

jag försökte berskriva ökningen per år. Var det fel tänkt?? Hur skulle jag kunna tänka så att det blir rätt om jag använde mig av min metod?

Ja precis, bra!

 och ff får du genom att ta $\frac{nytt värde}{tidigare värde}=\frac{30}{10}=3$ och ff=3 innebär ju 200 % ökning det också

Det är som Svante förklarade att du inte kan se tydligt i grafen om den ligger på ex. 12 %, 12,5 % eller 13 % vilket gör att du måste avrunda eller gissa lite för varje år du tittar på. Så du får små fel på varje år. När du sedan multiplicerar alla dessa små fel med varandra så blir det som uttrycket "Många bäckar små, gör en stor å" och i slutet hamnar du ganska mycket fel. Hade du haft mer exakta värden eller kunnat se tydligare med en mer detaljerad graf för varje år så hade din metod fungerat, men den hade ändå varit onödigt jobbigt och tidskrävande.

Jag kan såklart inte heller säga att den ligger på exakt 10 % 2000 eller exakt 30 % år 2010. Men i och med att jag bara gör två avrundningar så minimeras felen i detta fall, och gör inte så stor skada.

De är en fråga från nationella provet i åk9 2013. Vårt NP kommer handla om samband och förändring (procent). Vad tipsar du mig? Vart ska jag vara mest uppmärksam?? Finns det andra formel så som den du nyss skrev ” ff=nya värdet/gamla värdet” ?

Jag tycker i de trådar jag hjälpt dig i detta forumet har förstått och kan de  viktigaste metoderna för att räkna ut samband och förändringar. Jag tror mest du ska se till att vara noggrann med att läsa frågan och se till att du förstår vad de frågar efter och vad de menar så du undviker (som i det här fallet) att göra det krångligare än vad det är.

De formlerna som man oftast använder är de du brukar referera till $\frac{skilland(ökning/minskning)}{ursprungliga}$

och $ff=\frac{nytt värde}{gammlt värde}$

däremot något som egentligen är samma formel men när du ska jämföra två saker som är samtidigt

ex. Äpplena kostar 8 kronor och Päronen kostar 12 kronor kilot. Hur många procent mer kostar päronen än/jämfört med äpplena per kilo?

Då har du inte som du kan kalla för det "ursprungliga"

Då måste du vara noga med hur du ställer upp det. 

Hur många procent mer kostar päronen än/jämfört med äpplena? $\frac{skil\ln ad}{äpplenas kostnad}$=$\frac{12-8}{8}=\frac{4}{8}=50 \%$

I nämnaren sätter man då det som man ska jämföra med

Snarlik fråga hade varit om man vänder på det Hur många procent mindre kostar äpplena än/jämfört med päronen?

Det låter likt men har helt annat svar för då ska vi jämför med päronen $\frac{skil\ln ad}{päronens kos\mathrm{tn}ad}=\frac{4}{12}=25 \%$ 

Så där är det lätt att gå bort sig och du kan bli förvillad om du alltid försöker  tänka "skillnad"/ursprungliga" eftersom det inte alltid är en förändring över tid det handlar om

Isåfall fråga 9  skulle det vara rätt att lösa den på följande sätt :

skillnad/det vi gemför med = 80/90=0,888.. ungefär 89%.

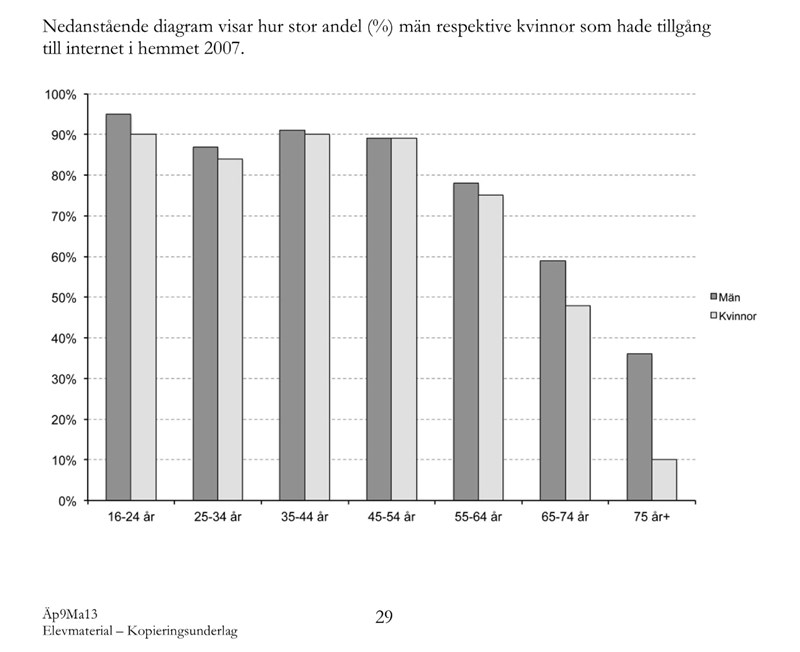
Ja precis där var ett likadant exempel som mitt med päron och äpplen där man måste tänka till vad det är man jämför med och det löste du rätt :)

det var länge sen jag skrev ett sådan typ av prov, känner mig därför ganska nervös. Förekommer det A frågor på provet eller är det C frågor?? 

Formelerna jag känner till är :

ff=nya värdet/gamla värdet

procentuell ökning elr sänkning : skillnad/ursprung

är det bara de som man behöver för att kunna lösa samtliga samband och förändrings uppgifter? :)

Jag vet faktiskt inte hur jag ska tänka på fråga 12 

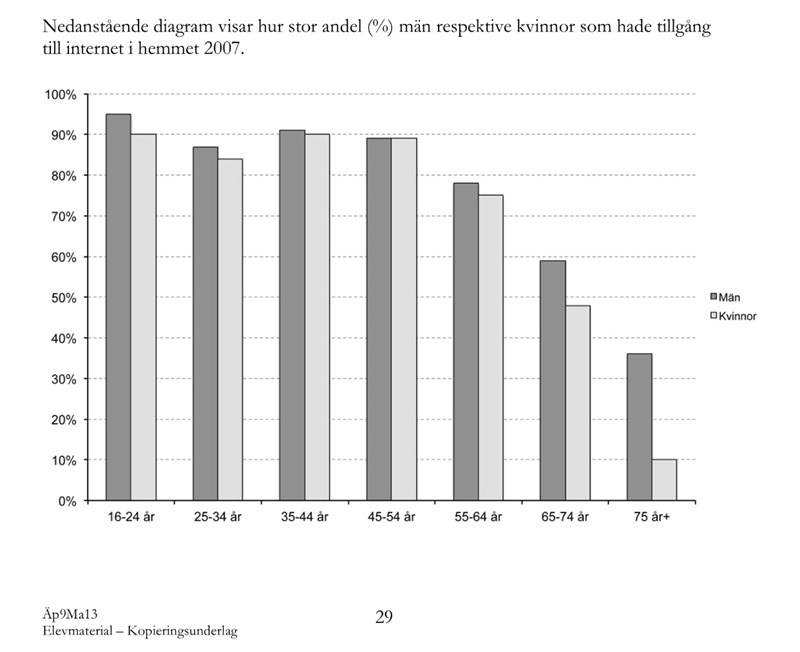
 Vilken formel ska jag använde i sånna typer av frågor??

Samma sätt som du gjorde nyss på fråga 9 bör funka!

Jag har inte gått i skolan på ett tag och heller inte undervisat i matematik nyligen men så vitt jag vet ska provet kunna testa på A-nivå, C-nivå och E-nivå.

På vissa uppgifter kan det vara så att de antingen är för E, C eller A-nivå och anpassade för det.

Vissa frågor kan gälla alla betygsstegen och beroende på hur väl, noggrant eller bra man löser det så kan man hamna på olika nivå.

Inga andra rena formler som jag kan komma på att man behöver. Sen kan det ibland vara så inför högre betyg att man ställs inför problem där man måste tänka till lite och kanske använda sina kunskaper på ett något annat sätt. Men de sakerna brukar lägga en bra grund för att lösa standraduppgifter.

Sen har vi ju såklart den klassiska: andel=$\frac{delen}{hela}$ men den är rätt given ju

I Matematik 1 så står följande delområden under samband och förändring:

Promille, ppm och procentenheter
Förändringsfaktor och index samt metoder för beräkning av räntor och amorteringar
Begreppen funktion, definitions- och värdemängd samt egenskaper hos linjära funktioner och potens- och exponentialfunktioner
Representationer av funktioner i form av ord, funktionsuttryck, tabeller och grafer
Skillnader mellan begreppen ekvation, olikhet, algebraiskt uttryck och funktion

https://sv.wikipedia.org/wiki/Matematik_1

Men jag vet inte alls om det gäller ert prov..

Jag kom på lösningen 

man tar (75-10)/75=0,8666... ungefär 87%

Tack så mycket för hjälpen!! Det uppskattas :)