är 2x radianen eller är svaret radianen dvs 1?
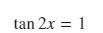
Vad får du om du räknar ut x i grader?
Laguna skrev:Vad får du om du räknar ut x i grader?
22.5
Laguna skrev:Vad får du om du räknar ut x i grader?
Så om jag fattat rätt så kommer svaret av sin tan cos termer vara den samma men uträckningen av det som står i parantesen blir olika beroende på om det är radian eller?
Hur många radianer är 22,5 grader?
Laguna skrev:Hur många radianer är 22,5 grader?
0.39???
Dvs pi/8
Vadå så man räknar ut i grader först sen översätter man?
Kanske, men det finns ett exakt uttryck, som innehåller . Då räknar man sällan ut talvärdet.
Bra, du hann skriva själv medan jag skrev det här.
Laguna skrev:Kanske, men det finns ett exakt uttryck, som innehåller . Då räknar man sällan ut talvärdet.
Finns det inget direkt sätt utan grader att få tag på radianen?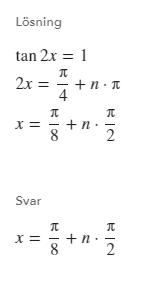
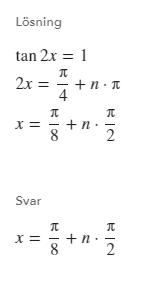
Man kan tänka i radianer direkt, om man är van.
Memorisera standardvinklarna! (Eller kolla i ditt formelblad, memorisera de brukar man inte behöva göra förrän universitet). De är helt enkelt en uppsättning vinklar som har trigonometriska värden som ofta används i uppgifter och har värden som inte ser så jobbiga ut på bråkform ( t.ex.)
Om du kollar i Skolverkets formelblad
(som du bland annat borde få ha på nationella prov och vanliga matematikprov också). Så ser du att finns i tabellen för trigonometriska värden med både motsvarande vinkel i grader och radianer listade.
Ett annat sätt att ”tänka” i radier utan att tänka i grader (som kanske inte är applicerbart just på denna uppgift i och för sig) är att komma ihåg att ett varv på enhetscirkeln motsvarar (eller ). Då kan du lätt lista ut hur långt ett halvt varv/180 grader är, respektive en fjärdedels varv, osv.
coffeshot skrev:Memorisera standardvinklarna! (Eller kolla i ditt formelblad, memorisera de brukar man inte behöva göra förrän universitet). De är helt enkelt en uppsättning vinklar som har trigonometriska värden som ofta används i uppgifter och har värden som inte ser så jobbiga ut på bråkform ( t.ex.)
Om du kollar i Skolverkets formelblad
(som du bland annat borde få ha på nationella prov och vanliga matematikprov också). Så ser du att finns i tabellen för trigonometriska värden med både motsvarande vinkel i grader och radianer listade.
Ett annat sätt att ”tänka” i radier utan att tänka i grader (som kanske inte är applicerbart just på denna uppgift i och för sig) är att komma ihåg att ett varv på enhetscirkeln motsvarar (eller ). Då kan du lätt lista ut hur långt ett halvt varv/180 grader är, respektive en fjärdedels varv, osv.
Radien är alltid 1, med sin och cos, varför ha med r finns det undantag?
AlexanderJansson skrev:coffeshot skrev:Memorisera standardvinklarna! (Eller kolla i ditt formelblad, memorisera de brukar man inte behöva göra förrän universitet). De är helt enkelt en uppsättning vinklar som har trigonometriska värden som ofta används i uppgifter och har värden som inte ser så jobbiga ut på bråkform ( t.ex.)
Om du kollar i Skolverkets formelblad
(som du bland annat borde få ha på nationella prov och vanliga matematikprov också). Så ser du att finns i tabellen för trigonometriska värden med både motsvarande vinkel i grader och radianer listade.
Ett annat sätt att ”tänka” i radier utan att tänka i grader (som kanske inte är applicerbart just på denna uppgift i och för sig) är att komma ihåg att ett varv på enhetscirkeln motsvarar (eller ). Då kan du lätt lista ut hur långt ett halvt varv/180 grader är, respektive en fjärdedels varv, osv.
Radien är alltid 1, med sin och cos, varför ha med r finns det undantag?
Om du menar varför jag skrev ”rad” när jag skrev i radianer så var det bara för att förtydliga att det var just radianer jag skrev i. ”rad”=förkortning för radianer. Jag la till det på samma sätt som man t.ex. lägger till Celsius på ett svar på en fysikuppgift som handlar om grader. Det hade inget med själva radien att göra.
Jag antar att du talar om radien i enhetscirkeln som hypotenusan (=långa sidan) av den triangel som bildas när du roterar x antal radianer från origo. I enhetscirkelns kontext stämmer det alltid att den sidan har längden 1, ja.
AlexanderJansson skrev:
Radien är alltid 1, med sin och cos, varför ha med r finns det undantag?
I enhetscirkeln är hypotenusan r alltid lika med 1, men för andra trianglar behöver det inte gälla.
Exempel: I den här generella rätvinkliga triangeln med sidlängder a, b och r så behöver r inte vara lika med 1.

För vinkeln v gäller det som bekant att
- sin(v) = a/r
- cos(v) = b/r
- tan(v) = a/b
För att lösa uppgiften kan man tänka "För vilken vinkel gäller att tangens för vinkeln är 1?"
EN sådan vinkel är ett åttondels varv, så 2x kan vara ett åttondels varv.
Ett åttondels varv är 45 grader om man vill använda enheten grader, eller pi/4 radianer om man vill använda enheten radianer.
EDIT - skrev något som jag nu ser att du redan hade koll på.



