5 svar

91 visningar

naytte behöver inte mer hjälp

Är detta en korrekt lösning?

Min strategi är att hitta hur stor kraftskillnaden mellan lådans tyngd och vattnets lyftkraft blir, för att se hur mycket tyngden måste öka för att det ska börja sjunka.

$V_{b o t t e n} = 0.01 m \cdot 0.35 m \cdot 0.18 m = 6.3 \cdot 10^{- 4} m^{3} m_{b o t t e n} = (6.3 \cdot 10^{- 4} m^{3}) \cdot (7900 k g / m^{3}) = 4.977 k g F_{g, b o t t e n} = 4.977 k g \cdot 9.82 m / s^{2}$

jag skriver inte ut hela $F_{g, b o t t e n}$ eftersom det blir för många decimaler.

$F_{l y f t} = 0.1386 m^{3} \cdot 1000 k g / m^{3} = 138.6 N$

Vattnet måste alltså tillföra en tyngd på $F_{l y f t} - F_{g, b o t t e n}$ för att lådan ska börja sjunka.

Då vill jag att den nya tyngdkraften, $F_{g, n y}$ , ska bli 138.6 N. Jag skriver upp detta på följande sätt:

$F_{g, n y} = (4.977 k g + m_{v a t t e n}) \cdot 9.82 m / s^{2} = 138.6 N \Rightarrow m_{v a t t e n} = (\frac{138.6}{9.82} - 4.977) k g$

även här undviker jag att skriva ut den tillförda vattnets massa eftersom jag skulle behöva avrunda.

Jag känner sedan till följande samband, vilket jag kan använda för att hitta hur stor volym vatten jag måste tillföra.

$m = ρ V \Rightarrow m_{v a t t e n} = ρ_{v a t t e n} \cdot V$

$(\frac{138.6}{9.82} - 4.977) k g = 1000 k g / m^{3} \cdot V V = \frac{(\frac{138.6}{9.82} - 4.977) k g}{1000 k g / m^{3}}$

Jag känner sedan tidigare till arean på plåten: $0.35 m \cdot 0.18 m = 0.063 m^{2}$

Det innebär att

$0.063 m^{2} \cdot D = V \Rightarrow 0.063 D = V 0.063 D = \frac{(\frac{138.6}{9.82} - 4.977) k g}{1000 k g / m^{3}} D = \frac{\frac{(\frac{138.6}{9.82} - 4.977) k g}{1000 k g / m^{3}}}{0.063} \approx 0.145 m = 14.5 c m$

Man måste alltså fylla vatten till höjden cirka 14.5 cm.

Ta till vara att använda dig av variabler så länge som möjligt. Sätt inte in några siffror förrän på slutet.

Rita en bild så att man ser vad du håller på med!

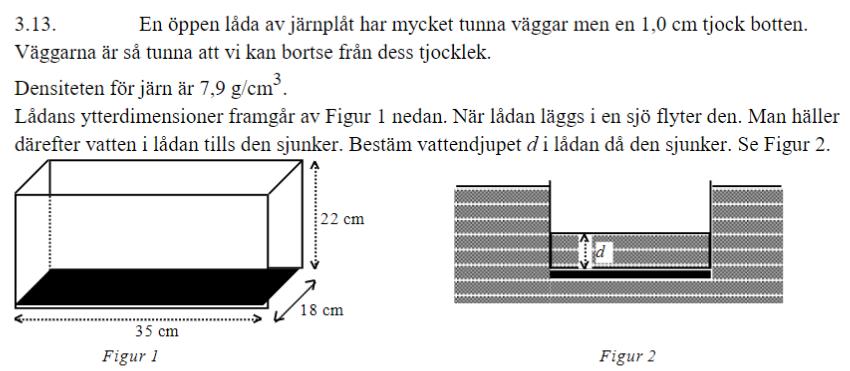
Alldeles innan man häller på den sista droppen vatten (som får lådan att sjunka) är lyftkraften för en skiva av vatten som är 22 cm högt lika stor som tyngden av en skiva som är d cm högt plus en skiva av järn med höjden 1 cm, alldeles oberoende av skivans area eller form, bara den har samma area oberoende av höjden.

$F_{lyft}=g\cdot A \cdot\rho_{vatten}\cdot22$

$F_{tyngd}=g\cdot A \cdot\rho_{vatten}\cdot d+g\cdot A \cdot\rho_{Fe}\cdot1$

Likställ krafterna och förkorta bort gA

$\rho_{vatten}\cdot22=\rho_{vatten}\cdot d+\rho_{Fe}\cdot1$

$d=\frac{\rho_{vatten}\cdot22-\rho_{Fe}\cdot1}{\rho_{vatten}}$

Jag väljer att räkna höjden i cm och densiteten i g/cm3 så blir det enklare siffror.

d=(1^.22-7,9.1)/1 = 14,1 cm.

Skillnaden mellan din lösning och min är nog avrundning.

Smaragdalena skrev:
Ta till vara att använda dig av variabler så länge som möjligt. Sätt inte in några siffror förrän på slutet.

Rita en bild så att man ser vad du håller på med!

Alldeles innan man häller på den sista droppen vatten (som får lådan att sjunka) är lyftkraften för en skiva av vatten som är 22 cm högt lika stor som tyngden av en skiva som är d cm högt plus en skiva av järn med höjden 1 cm, alldeles oberoende av skivans area eller form, bara den har samma area oberoende av höjden.

$F_{lyft}=g\cdot A \cdot\rho_{vatten}\cdot22$

$F_{tyngd}=g\cdot A \cdot\rho_{vatten}\cdot d+g\cdot A \cdot\rho_{Fe}\cdot1$

Likställ krafterna och förkorta bort gA

$\rho_{vatten}\cdot22=\rho_{vatten}\cdot d+\rho_{Fe}\cdot1$

$d=\frac{\rho_{vatten}\cdot22-\rho_{Fe}\cdot1}{\rho_{vatten}}$

Jag väljer att räkna höjden i cm och densiteten i g/cm3 så blir det enklare siffror.

d=(1^.22-7,9.1)/1 = 14,1 cm.

Skillnaden mellan din lösning och min är nog avrundning.

Det var så som uppgiften löstes i facit, och i facit blev det samma svar som du fick. Men jag förstår inte varför mitt svar (som inte avrundas någonstans förrän precis i slutet) blir lite högre än ditt.

Då får jag översätta ditt stora uttryck med alla siffrorna i till variabler, så att det går att se vad du har gjort...

138,6 = F_lyft = 0,1386 m³*1000 kg/m³ har enheten kg, inte N och är egentligen massan för 1 m vatten med tvärsnittsarean A, d v s $A\rho_{vatten}$

9,82 = g (enhet N/kg). Du borde ha multiplicerat, inte dividerat.

4,977 lådans massa i kg = $A(1cm)\rho_{Fe}$

0,063 är lådans tvärsnittsarea A

Eftersom din första parentes har enheter som inte stämmer så försöker jag inte skriva ditt uttryck.

Smaragdalena skrev:
Då får jag översätta ditt stora uttryck med alla siffrorna i till variabler, så att det går att se vad du har gjort...

138,6 = F_lyft = 0,1386 m³*1000 kg/m³ har enheten kg, inte N och är egentligen massan för 1 m vatten med tvärsnittsarean A, d v s $A\rho_{vatten}$

9,82 = g (enhet N/kg). Du borde ha multiplicerat, inte dividerat.

4,977 lådans massa i kg = $A(1cm)\rho_{Fe}$

0,063 är lådans tvärsnittsarea A

Eftersom din första parentes har enheter som inte stämmer så försöker jag inte skriva ditt uttryck.

Jag ska skriva upp allting i uttryck med variabler istället för det verkar vara svårt att tyda vad jag har gjort.

Strategin går som sagt ut på att hitta hur mycket tyngden på allting måste öka för att det ska sjunka.

${\vec{F}}_{s j u n k} = 9.82 (m_{p l å t} + m_{v a t t e n})$

Jag vill att det ovanstående uttrycket ska bli lika stort som lyftkraften är. Då vill jag alltså ha följande likhet:

${\vec{F}}_{s j u n k} = {\vec{F}}_{l y f t} \Rightarrow g (m_{p l å t} + m_{v a t t e n}) = ρ_{v a t t e n} \cdot g \cdot V_{u n d a n t r ä n g t v a t t e n} \Rightarrow (m_{p l å t} + m_{v a t t e n}) = ρ_{v a t t e n} \cdot V_{u n d a n t r ä n g t v a t t e n}$

Av detta får jag ut vilken massa vattnet ska ha för lyftkraften ska vara lika stor som tyngdkraften. Följande samband är känt:

$m = ρ V \Rightarrow m_{p l å t} + (ρ_{v a t t e n} \cdot V_{v a t t e n i l å d a n}) = ρ_{v a t t e n} \cdot V_{u n d a n t r ä n g t v a t t e n}$

När jag har löst ut volymen av vattnet i lådan kan jag dela den på arean av plåten och då borde jag få rätt svar.

$V_{v a t t e n i l å d a n} = \frac{(ρ_{v a t t e n} \cdot V_{u n d a n t r ä n g t v a t t e n}) - m_{p l å t}}{ρ_{v a t t e n}}$

$d = \frac{V_{v a t t e n i l å d a n}}{A_{p l å t}} = \frac{\frac{(ρ_{v a t t e n} \cdot V_{u n d a n t r ä n g t v a t t e n}) - m_{p l å t}}{ρ_{v a t t e n}}}{A_{p l å t}}$

$d = \frac{\frac{(1000 \cdot 0.35 \cdot 0.18 \cdot 0.22) - (0.01 \cdot 0.35 \cdot 0.18) \cdot 7900}{1000}}{0.35 \cdot 0.18} d = 0.141 m = 14.1 c m$

Oj, ser man på, nu fick jag rätt svar. Det verkar vara smart att inte sätta in värden förrän i slutet. Tack!

Sätt inte in värdena på slutet, och ha koll på enheterna! Då hittar man de flesta fel man har gjort (för det gör man ibland...).

Svara

Visa senaste svar