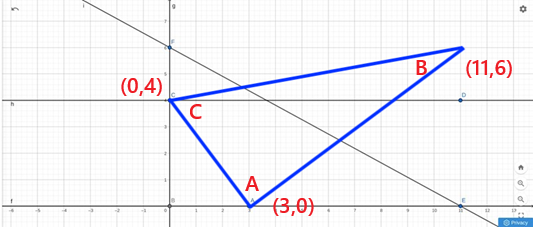
Är en triangel med hörn i punkterna (3,0) (0,4) och (11,6) rätvinklig? (Matematik/Matte 2/Logik och geometri)

Rita! Det är alltid bra och tar inte lång tid. Sedan kan du klura och räkna.

Ska jag rita ett koordinatsystem?

Tjenare det är Ahmed skrev:
Ska jag rita ett koordinatsystem?

Det låter som en bra idé. Markera de givna punkterna, ta en linjal och dra tre streck för att få en triangel.

Då får du en uppfattning direkt vad du har framför dig.

Är detta rätt ritat?

Jag har för mig att man även kan använda sig av pythagoras sats. Hur fungerar det?

Tjenare det är Ahmed skrev:

Är detta rätt ritat?

A och C är dina (3,0) och (0,4).

(11,6) saknas och vad de andra punkterna och linjerna är vet jag inte.

Tjenare det är Ahmed skrev:
Jag har för mig att man även kan använda sig av pythagoras sats. Hur fungerar det?

Då använder man sig av Avståndsformeln

Hur hade jag gjort det i denna uppgiften? Jag har tre olika koordinater.

Tjenare det är Ahmed skrev:
Hur hade jag gjort det i denna uppgiften? Jag har tre olika koordinater.

En triangel har tre sidor.

Ja, så hur ska jag använda denna formel till triangeln? Vi nämnde pythagoras sats, men sen så kom vi vidare till avståndsformeln. Hur gör jag?

Tjenare det är Ahmed skrev:
Ja, så hur ska jag använda denna formel till triangeln? Vi nämnde pythagoras sats, men sen så kom vi vidare till avståndsformeln. Hur gör jag?

Beräkna längder på triangelns sidor. Använd sedan Pythagoras sats.

Utifrån koordinaterna? Isåfall vet jag inte hur man gör

För en sida i taget: sätt in hörnens koordinater i avståndsformeln.
Så får du sidans längd.
När du har alla sidornas längder prövar du dem i Pythagoras sats.

Tjenare det är Ahmed skrev:

Är detta rätt ritat?

Nej. Det är ju inte ens en triangel...

Louis skrev:
För en sida i taget: sätt in hörnens koordinater i avståndsformeln.
Så får du sidans längd.
När du har alla sidornas längder prövar du dem i Pythagoras sats.

Här kan vi inte använda Pythagoras sats, eftersom den bara gäller för rätvinkliga trianglar.
I så fall måste vi först visa att triangeln är rätvinklig…

Men även omvändningen till Pythagoras sats gäller:
Om c² = a² + b² , där a, b och c är sidlängderna i en triangel, så är triangeln rätvinklig.
Den kan vi använda om den ingår i kursen. Annars får vi först bevisa den!

Enklast är väl ändå att kolla lutningen på sidorna (k-värdena) för att se om någon av vinklarna i triangeln är rät.

Men även omvändningen till Pythagoras sats gäller: Om c² = a² + b² , där a, b och c är sidlängderna i en triangel, så är triangeln rätvinklig.

Det var det jag menade.

I just den här uppgiften med dess koordinatvärden kan man snabbt se att triangeln är rätvinklig.
De tre mindre trianglarna är alla kongruenta. alfa + beta = 90^o.

Det är många som är ivriga att hjälpa till här, så det kan bli lite rörigt. Det går fint att använda avståndsformeln, eller pythagoras, eller beräkna linjernas lutning, ... De är olika varianter av samma princip.

Hur som helst var min tanke att du först skulle se triangeln framför dig, istället för bara tre givna koordinater i uppgiften. Gör man inte det blir allt superabstrakt när det diskuteras lösningsförlag för en uppgift man kanske inte ens har koll på.

Nu var Pieter snäll och ritade upp triangeln åt dig:

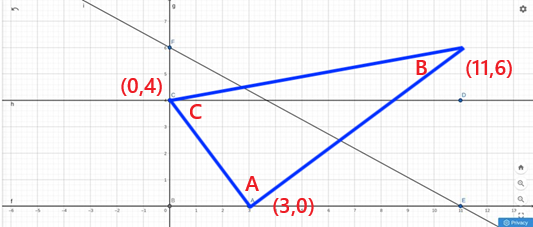
Jag har kallat vinklarna för A, B och C. Det ser ju ut som om A skulle kunna vara rätvinklig. Vi får testa det!

(Medan jag skriver detta inlägg så har en annan redan postad svaret, men jag fortsätter.)

Nu när vi ser triangeln så kan vi använda avståndsformeln för att beräkna sidornas längd.

$A B = \sqrt{{(11 - 3)}^{2} + {(6 - 0)}^{2}} = \sqrt{64 + 36} = \sqrt{100} = 10$

Sedan fortsätter man med att beräkna AC och BC på samma sätt.

När du har de tre sidorna kan du kontrollera med pythagoras. Om AB²+AC²=BC² så är triangeln rätvinklig. Stämmer det inte så är den inte det.

Visa spoiler

$A C = \sqrt{{(3 - 0)}^{2} + {(0 - 4)}^{2}} = \sqrt{3^{2} + {(- 4)}^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5 B C = \sqrt{{(11 - 0)}^{2} + {(6 - 4)}^{2}} = \sqrt{11^{2} + 2^{2}} = \sqrt{125}$

Vi testar med pythagoras:

$A B^{2} + A C^{2} = B C^{2} 10^{2} + 5^{2} = {(\sqrt{125})}^{2} 100 + 25 = 125 125 = 125$

Triangeln är rätvinklig!

Det nämndes även att man kan räkna ut lutningen (k-värdet i y=kx+m) för AB och AC. Här har du den varianten också, men dold om du vill försöka själv först:

Visa spoiler

$k_{A B} = \frac{∆ y}{∆ x} = \frac{6 - 0}{11 - 3} = \frac{6}{8} k_{A C} = \frac{∆ y}{∆ x} = \frac{0 - 4}{3 - 0} = \frac{- 4}{3}$

Nu måste man veta att två linjer är vinkelräta om deras k-värden multiplicerar till -1. Vi provar:

$k_{A B} \times k_{A C} = \frac{6}{8} \times \frac{- 4}{3} = \frac{6 \times (- 4)}{8 \times 3} = \frac{- 24}{24} = - 1$

Nu har vi återigen visat att triangeln är rätvinklig.

sictransit skrev:
Det är många som är ivriga att hjälpa till här, så det kan bli lite rörigt. Det går fint att använda avståndsformeln, eller pythagoras, eller beräkna linjernas lutning, ... De är olika varianter av samma princip.

Hur som helst var min tanke att du först skulle se triangeln framför dig, istället för bara tre givna koordinater i uppgiften. Gör man inte det blir allt superabstrakt när det diskuteras lösningsförlag för en uppgift man kanske inte ens har koll på.

Nu var Pieter snäll och ritade upp triangeln åt dig:

Jag har kallat vinklarna för A, B och C. Det ser ju ut som om A skulle kunna vara rätvinklig. Vi får testa det!

(Medan jag skriver detta inlägg så har en annan redan postad svaret, men jag fortsätter.)

Nu när vi ser triangeln så kan vi använda avståndsformeln för att beräkna sidornas längd.

$A B = \sqrt{{(11 - 3)}^{2} + {(6 - 0)}^{2}} = \sqrt{64 + 36} = \sqrt{100} = 10$

Sedan fortsätter man med att beräkna AC och BC på samma sätt.

När du har de tre sidorna kan du kontrollera med pythagoras. Om AB²+AC²=BC² så är triangeln rätvinklig. Stämmer det inte så är den inte det.

Visa spoiler

$A C = \sqrt{{(3 - 0)}^{2} + {(0 - 4)}^{2}} = \sqrt{3^{2} + {(- 4)}^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5 B C = \sqrt{{(11 - 0)}^{2} + {(6 - 4)}^{2}} = \sqrt{11^{2} + 2^{2}} = \sqrt{125}$

Vi testar med pythagoras:

$A B^{2} + A C^{2} = B C^{2} 10^{2} + 5^{2} = {(\sqrt{125})}^{2} 100 + 25 = 125 125 = 125$

Triangeln är rätvinklig!

Det nämndes även att man kan räkna ut lutningen (k-värdet i y=kx+m) för AB och AC. Här har du den varianten också, men dold om du vill försöka själv först:

Visa spoiler

$k_{A B} = \frac{∆ y}{∆ x} = \frac{6 - 0}{11 - 3} = \frac{6}{8} k_{A C} = \frac{∆ y}{∆ x} = \frac{0 - 4}{3 - 0} = \frac{- 4}{3}$

Nu måste man veta att två linjer är vinkelräta om deras k-värden multiplicerar till -1. Vi provar:

$k_{A B} \times k_{A C} = \frac{6}{8} \times \frac{- 4}{3} = \frac{6 \times (- 4)}{8 \times 3} = \frac{- 24}{24} = - 1$

Nu har vi återigen visat att triangeln är rätvinklig.

Intressant, nu förstår jag!

Tack för all hjälp allihopa!

Dock en sista fråga bara till dig sictransit.

Jag kan lätt slarva mig på matteprov, vill dock bara dubellkolla med dig. När du använde dig av pythagoras sats och räknade ut BC så löste du inte roten ur 125 som resterande AB och AC, utan slutade där. Jag känner mig själv och vet att jag hade löst den och fått 11,18 och sedan till slut 124,9 och därmed blivit osäker på mitt svar. Hur vet jag när jag ska göra som du gjorde och inte fortsätta? Är det när svaret blir med decimal? Eller ska jag bara avrunda?

Tjenare det är Ahmed skrev:

När du använde dig av pythagoras sats och räknade ut BC så löste du inte roten ur 125 som resterande AB och AC, utan slutade där. Jag känner mig själv och vet att jag hade löst den och fått 11,18 och sedan till slut 124,9 och därmed blivit osäker på mitt svar. Hur vet jag när jag ska göra som du gjorde och inte fortsätta? Är det när svaret blir med decimal? Eller ska jag bara avrunda?

Man behöver inte lösa roten. Det går bra utan att avrunda och utan räknare:

AB² = (11-3)² + 6² = 64 + 36 = 100
AC² = 3² + 4² = 9 + 16 = 25
BC² = 11² + (6-4)² = 121 + 4 = 125

Jaha, ser det ut så här då istället?

(√100)²+ (√25)² = (√125)²

100+25=125

Tjenare det är Ahmed skrev:
Intressant, nu förstår jag!

Tack för all hjälp allihopa!

Dock en sista fråga bara till dig sictransit.

Jag kan lätt slarva mig på matteprov, vill dock bara dubellkolla med dig. När du använde dig av pythagoras sats och räknade ut BC så löste du inte roten ur 125 som resterande AB och AC, utan slutade där. Jag känner mig själv och vet att jag hade löst den och fått 11,18 och sedan till slut 124,9 och därmed blivit osäker på mitt svar. Hur vet jag när jag ska göra som du gjorde och inte fortsätta? Är det när svaret blir med decimal? Eller ska jag bara avrunda?

Om jag får √125 som ett svar på en fråga där uppgiften inte bett mig att svara exakt, så beräknar jag det till exempelvis ≈11,2 (med korrekt antal värdesiffror). Gäller det en spänning så är säkert 11,2 V rimligare än √125 V.

Om jag däremot får med mig √125 som en del av en uträkning så finns det absolut ingen anledning att beräkna och avrunda. Det ger mig bara en massa decimaler jag måste ta ställning till och jag förlorar precision. Känner jag dessutom på mig att jag snart skall kvadrera värdet, så vet jag ju att jag snart får tillbaka min 125:a. Se mitt sista inlägg i den här tråden om 12π vs ungefär 37,68: https://www.pluggakuten.se/trad/volym-pa-kon-3/

Om jag som i uppgiften har ett √100 så förlorar jag dock ingenting på att skriva 10 istället.

Om jag har en tumregel så är den: Räkna enbart ut något om du måste eller kan göra det utan att förlora precision.

Tackar!