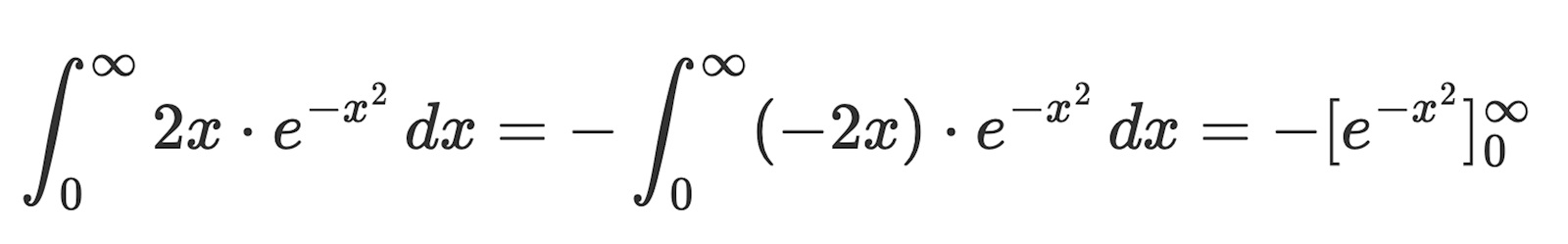Är följande generaliserade integraler konvergenta?
Min uppgift:
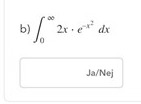
Jag började att räkna med partiell integration, men jag förstår inte hur man tar primitiv funktion eller derivata av e^(-x^2) och den partiella integrationen blir svår att räkna ut.
Partiell integrering tror jag inte är så bra här. Vad sägs om ett variabelbyte? Vad tror du om ?
Men då blir det två olika variabler när jag skriver primitiva. Jag skrev integralen från 0 till t för 2xe^(u) och fick t^2*e^(t). Vad gör jag nu?
Notera att 2x är "nästan" den inre derivatan av -x^2
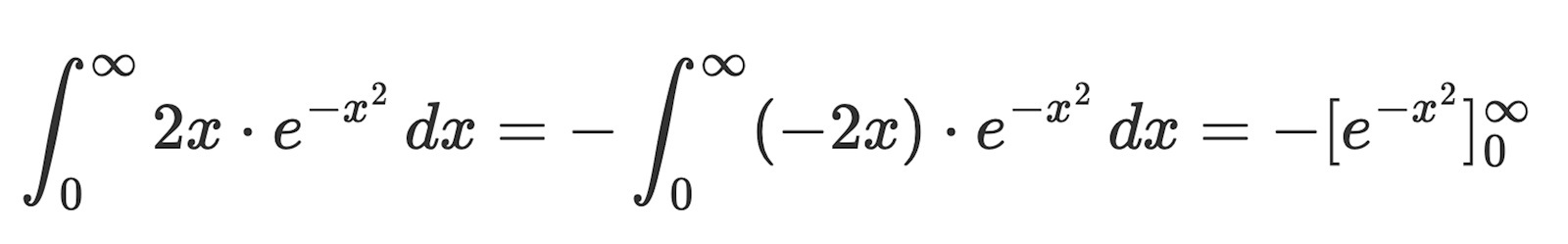
Jag förstår inte riktigt vad du menar, Anna. Mitt förslag är följande:
Ta fram primitiv, skriv om i termer av igen och beräkna.
Trinity2 jag förstår nu men hur är det "nästan", det är väll exakt derivatan? (-2x)*e^(-x^2) är derivatan av e^(-x^2)
Trinity2 skrev:Notera att 2x är "nästan" den inre derivatan av -x^2
Trinity2 jag förstår nu men hur är det "nästan", det är väll exakt derivatan? (-2x)*e^(-x^2) är derivatan av e^(-x^2)
Han förlängde ju med -1!
jaha jag förstår nu tack
Bara så att du är med på det: mitt förslag och Trinitys förslag är identiska! Det är bara att jag rekommendare ett variabelbyte medan Trinity struntade i det mellansteget.
Är det här rätt om jag då använder variabelbyte?:
naytte skrev:Bara så att du är med på det: mitt förslag och Trinitys förslag är identiska! Det är bara att jag rekommendare ett variabelbyte medan Trinity struntade i det mellansteget.
Ja, men det är x som går mellan 0 och "oändligheten".
Anna000 skrev:Är det här rätt om jag då använder variabelbyte?:
Det är fel på tecknen, e^(-u) skall det vara.
Svaret är dock rätt.
Nej, det är rätt tecken så som Anna skrev. Hon lät u=-x^2 isället. Det är ju ett minustecken framför integraltecknet.
naytte skrev:Nej, det är rätt tecken så som Anna skrev. Hon lät u=-x^2 isället. Det är ju ett minustecken framför integraltecknet.
e^oo kommer aldrig att vara 0
Nej, jag håller med. Men felet är som sagt att det är som går från till och inte .
Om man låter det gå till rätt värde på , dvs. till , blir det ju rätt.