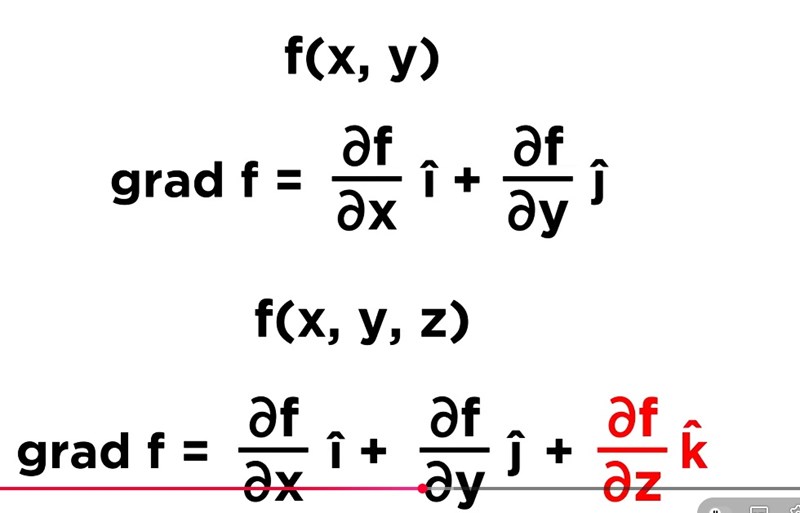Är gradienten för en funktion typ exakt samma som en linjärkombination fast med d/d(variabel)?

Asså kolla jag har  sett de här paranteserna [], [), (], (), {} men inte <>

Ahh är det bara för vektorform <>, men varför, vanliga paranteser funkar väl?

Kan du visa ett exempel?

Det kanske råder lite begreppsförvirring här kring vad en linjärkombination är. $\mathbf{i}$, $\mathbf{j}$ och $\mathbf{k}$ är enhetsvektorerna i $x$-, $y$- och $z$-riktning. Ett annat sätt att skriva det på är

$\displaystyle \mathrm{grad} f = \nabla f\left(x,y,z\right) =\left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)$

naytte skrev:

Det kanske råder lite begreppsförvirring här kring vad en linjärkombination är. $\mathbf{i}$, $\mathbf{j}$ och $\mathbf{k}$ är enhetsvektorerna i $x$-, $y$- och $z$-riktning. Ett annat sätt att skriva det på är

$\displaystyle \mathrm{grad} f = \nabla f\left(x,y,z\right) =\left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)$

såå... är det en linjärkombination hehe?

Nej. Eller, vad menar du med det? Det är bara en vektor. Alla vektorer är ju trivialt linjärkombinationer av rummets basiselement.

Hur såg det ut när du såg < >?

Aja kanske inte behöver tänka på det med om det är linjärkombination eller inte. Nämen jag har bara sett den parantesen lite överallt men vet inte varför/när.

Vissa författare skriver vektorer med < > istället för ( ).

naytte skrev:

Vissa författare skriver vektorer med < > istället för ( ).

Men är det verkligen samma sak, är det inte mer konventionellt att bara ha en istället?

Det är bara konvention. Det spelar ingen roll. Men < > används också för det man kallar för inre produkt så det kan leda till förvirring att envisas med att notera vektorer med < >.

naytte skrev:

Det är bara konvention. Det spelar ingen roll. Men < > används också för det man kallar för inre produkt så det kan leda till förvirring att envisas med notera vektorer med < >.

Vad är det för något? Det får mig att tänka på inre/yttre värden för x eller vad det nu var igen i envariabeln?