Är rörelsemängdsmoment beroende av referensram?
Halloj!
Jag funderar lite på rörelsemängdsmoment och på ett exempel där någon betraktar en människa från rymden. Låt säga att en människa står på ekvatorn med massa och en observatör ser henne ovanifrån från rymden:
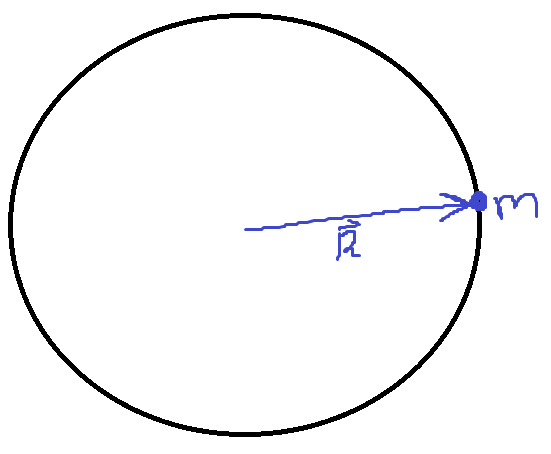
För en observatör från rymden ser det ut som att människan genomgår en cirkelrörelse moturs med tangentialfarten . Eftersom hon jämfört med jorden i princip är en punktmassa skulle observatören från rymden tycka att hon med avseende på jordens rotationsaxel har rörelsemängdsmoment:
där är enhetsvektorn i den positiva -riktningen (ut mot oss).
Människan på ekvatorn tycker däremot inte att hon rör sig överhuvudtaget, i hennes referensram står hon still.
Betyder detta att begreppet "rörelsemängdsmoment" är knutet direkt till vilken referensram man observerar ur? Dvs. människan tycker att hon saknar rörelsemängdsmoment, medan observatören från rymden tycker att hon har ett.
Ja, som ditt tankeexperiment illustrerat så är rörelsemängdsmomentets storlek och riktning referensramsberoende.
Alla storheter som definieras med hänvisning till en referensram är per definition 'referenramsberoende'. Sedan så kan storheter vara bevarade eller identiska under vissa specifika kategorier av referensramsbyten (basbyten).
Acceleration är exempelvis uppenbart referensberoende eftersom den härleds från förskjutning och hastighet vilka definieras relativt en referensrams stillastående objekt ('axlarna'). Sedan råkar det vara så att ett objekts acceleration ändå är lika stor i alla referenssystem som rör sig med konstant hastighet relativt varandra och som inte roterar. Så en person i och utanför ett tåg med konstant fart är överens om att kroppar faller mot marken med acceleration 9.8 m/s^2. Men involverar vi accelererande referensramar så är inte accelerationer nödvändigtvis lika -- en person i en fallande hiss tycker kanske att bollar faller mot marken med 0 m/s^2 när de utanför tycker samma boll faller med 9.82 m/s^2.
Alla storheter beror av referensram men själva fysikens lagar (differentialekvationerna som beskriver sambanden mellan storheterna) är referensramsoberoende så länge vi avgränsar oss till referensramar som rör sig med konstant hastighet relativt varandra.



