Är TOTAL entropi en monotont växande funktion av TOTAL energi?

Hej!

Jag håller på att läsa om några relevanta delar i andra utgåvan av Callen och har en fundering om hans tredje postulat:

Postulate III. The entropy of a composite system is additive over theconstituent subsystems. The entropy is continuous and differentiable and is amonotonically increasing function of the energy.

När jag först läste detta postulat tolkade jag det som att Callen menar att för varje enskilt delsystem $\alpha$ med entropfunktion $S^{(\alpha)}=S\left(U^{(\alpha)},V^{(\alpha)},\dots\right)$ så skall följande gälla:

$\displaystyle \frac{\partial S^{(\alpha)}}{\partial U^{(\alpha)}}>0$

På vidare läsning tror jag dock inte att det var detta han nödvändigtvis(?) menade. I kapitel 5 diskuterar Callen det som kallas för energiminimeringsprincipen, som säger att en fri termodynamisk koordinat vid fixerad entrpi $S$ antar det värde som minimerar den interna energin över mångfalden av tillstånd med entropi $S$. I sin motivering till denna princip diskuterar han utseendet på entropiytan för ett sammansatt system med två delsystem, där axlar utan superscript betecknar TOTALA parameterar i det sammansatta systemet medan superscript $(1)$ betecknar parameterar i delsystem 1:

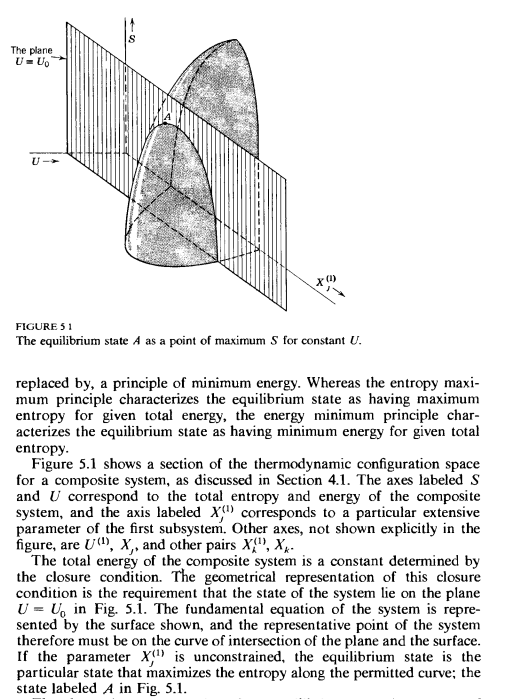
Han skriver i sin diskussion:

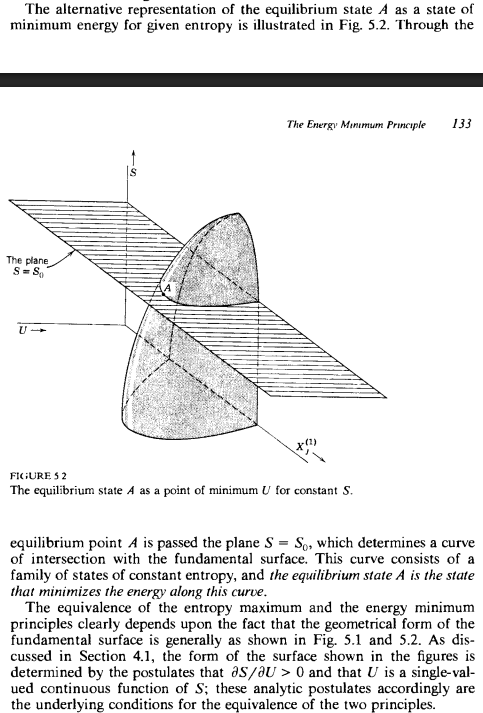
Det verkar alltså som att han med sitt tredje postulat menade att den TOTALA entropin är en monotont växande funktion av den TOTALA energin, men jag är inte riktigt säker. Därför har jag två frågor:

• Anta att vi har ett system med två delsystem. Gäller det då att $\displaystyle \frac{\partial S^{(1)}}{\partial U^{(1)}}>0$ OCH $\displaystyle \frac{\partial S^{(2)}}{\partial U^{(2)}}>0$?
• Anta att vi har ett system med två delsystem som har sammanlagd entropi $S$ och sammanlagd energi $U$. Gäller det då att $\displaystyle \frac{\partial S}{\partial U}>0$?