arccot(-1)
Jag blir lite osäker... visst det är så att man kan inte ta arccot på -1 för att den är odefinierad för negativa värden?
Jag har uppgiften:
och arccot(-1) dyker upp direkt.
Man brukar definiera den vackra och spänstiga funktionen så att definitionsmängden och värdemängden
Edit: Det finns andra definitioner, men denna ger ingen diskontinuitet i 0.
God morgon och tack för svaret!
Vackra och spänstiga 😊? Enligt min kurslitteratur är hon tråkigt och oanvändbar, och måste ersättas med så fort hon dyker upp!
Ja, det sambandet gäller eftersom
Just det!
Tack King of Math!
dajamanté skrev:God morgon och tack för svaret!
Vackra och spänstiga 😊? Enligt min kurslitteratur är hon tråkigt och oanvändbar, och måste ersättas med så fort hon dyker upp!
Ja, men det finns lite finlir här. Du har definierat som den inversa funktionen till restriktionen av funktionen till intervallet .
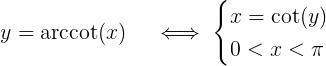
Det kan vara bra att känna till att alla inte tycker att arccot(-1) ska tolkas på samma sätt. Så här ser y=arccot(x) ut enligt Desmos (och din definition, ingen diskontinuitet i 0)
.jpg?width=800&upscale=false)
Detta kan jämföras med plot arccot(x), x=-2pi to 2pi i Wolfram.
.jpg?width=800&upscale=false) Notera att Desmos och Wolfram är lite ovänner om vad som händer då x<0.
Notera att Desmos och Wolfram är lite ovänner om vad som händer då x<0.
Wolfram och Desmos ovänner! Det är en trist dag för matematik! ... men vad säger Geogebra då ?
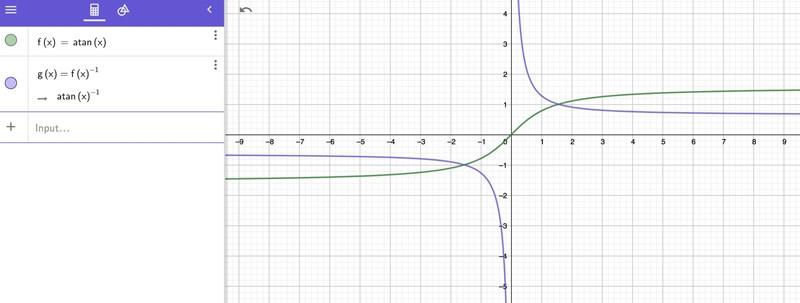
... hon säger som Wolfram. Och dem verkar överens med Mathematica.
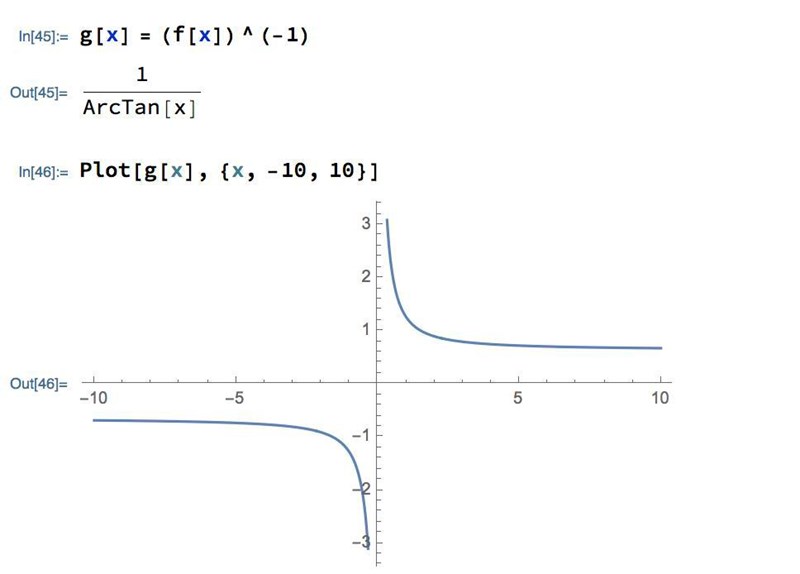
Jag känner en hemsk vertigo som sätter sig i mitt kropp. Hur kan man klara det om även datorer är inte överens i analys!!

Jättefina grafer och bra att du börjat jobba med Mathematica. Nu väntar jag bara på att du ska hitta funktioner som ReflectionMatrix[] och RotationMatrix[] :)
Men jag har ett klagomål!
När du jobbar med inversa funktioner måste du tänka på att i regel inte är samma sak som , ty . En funktion har en invers om den är injektiv. En sådan funktion kallas omvändbar. Inversen definieras alltså av
.
Genom att införa definitionsmässiga restriktioner på intervallen för tan- och cotangensfunktionerna erhåller vi omvändbara funktioner som uppfyller kraven för den dubbla implikationspilen. Slutligen ett numeriskt exempel på hur inversen och invertering inte är samma sak
Guggle skrev:Jättefina grafer och bra att du börjat jobba med Mathematica. Nu väntar jag bara på att du ska hitta funktioner som ReflectionMatrix[] och RotationMatrix[] :)
God morgon!
Du borde ha sett min sista babysbyte i Smutstvätts tråd, matriser viftades höger och vänster! Jag upptäckte RotationMatrix[], blodet och svett ska inte längre rinna längs pannan!
ReflectionMatrix[] har jag precis tittat på... OMG, så många timmar kunde ha varit räddat...
Men jag har ett klagomål!
När du jobbar med inversa funktioner måste du tänka på att i regel inte är samma sak som , ty . En funktion har en invers om den är injektiv. En sådan funktion kallas omvändbar. Inversen definieras alltså av
.
Genom att införa definitionsmässiga restriktioner på intervallen för tan- och cotangensfunktionerna erhåller vi omvändbara funktioner som uppfyller kraven för den dubbla implikationspilen. Slutligen ett numeriskt exempel på hur inversen och invertering inte är samma sak
Jag... är inte säker att jag förstår.
Jag förstår delen med att restriktioner är nödvandiga innan man inverterar trigonometriska funktioner. Men inte riktig delen:
Jag har ritat och jo, det ser olika ut men jag skulle inte ha gissat själv att . $$\cot(-\sqrt3)}$$ inte ens dyker upp på grafen, den impolite brat.
dajamanté skrev:Jag... är inte säker att jag förstår.
men jag skulle inte ha gissat själv att
Jag försökte förklara två saker på samma gång, typisk flum-pedagogik från Guggle!
1) Alla programvaror är inte överens om restriktionen av trigonometriska funktioner och kommer därför ge dig olika värden på t.ex. arccot(x), när x<0. Men det är inte konstigare än att man har olika uppfattning om en vinkel är -30° eller 330°
2) Den inversa funktionen är INTE den inverterade funktionen. Detta kan man visa med exempel
Låt
Då gäller
Detta är INTE samma sak som
Ja, nu ser jag. Tack!
(och jo, det är konstigare!)




