Aritmetisk summa av rekursiv formel
Hej!
hur är det tänkt att man ska beräkna Summan av de 25 första elementen när man enbart har tillgång till dess rekursiva formel?
för man måste ju räkna ut alla tal innan man kommer till det 25:e för att ens få vad det sista talet är, och det verkar otroligt onödigt mycket jobb, så det måste finnas något annat sätt tänker jag?
men hur då?
Säg du har den aritmetiska formeln f(n) = 3(n-1) + 1, och du ska beräkna summan av de första 5 elementen i talföljden. Första elementet blir då när n=1, som är lika med 1: f(1) = 1. Sista elementet blir f(5) = 13.
Om vi skriver ut de första 5 elementen i talföljden: 1, 4, 7, 10, 13
Så ser vi att summan blir (1+13) + (4+10) + (7) = 14 + 14 + 7 = 35
En formel som man kan alltid använda är det här (gäller dock bara aritmetiska talföljder):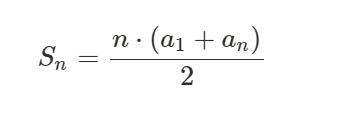
där a1 är första talet i talföljden, an är det n:te talet som man söker för och där n är figurnummer. Om du lägger samma värden i den här formeln så får du även att summan blir 35.
jag vet att b1=4
formeln är bn=11+bn-1 för n är större än eller lika med 2
kan jag lägga in hela den formeln för a2 i formeln för den aritmetiska summan?
KlmJan skrev:jag vet att b1=4
formeln är bn=11+bn-1 för n är större än eller lika med 2
kan jag lägga in hela den formeln för a2 i formeln för den aritmetiska summan?
Oh, juste det är en rekursiv formel! Aj men glöm det jag sa då, helt fel av mig... sorry trött asså. Du behöver ju veta sista termens värde för att kunna utföra det. Jag vet faktiskt inte hur man skulle kunna gå tillväga här, eller kanske jag är bara för trött för att fatta
det är ok, tack ändå! är trött nu så går segt att fatta grejer. men det är bara o kämpa på :)
Men vänta, nu när jag tänker på det, borde inte det rekursiva formeln omskrivas till den aritmetiska formeln f(n) = 4 + 11(n-1)? Med det så skulle du kunna beräkna summan om du följer formeln?
det är det jag itne fattar. Hur i hela världen går man tillväga för att skriva om en rekursiv formel till en aritmetisk formel? Det hade gjort hela uppgiften 100 gånger enklare.
Deluppgiften inna nvar med en aritmetisk formel och den löste jag busenkelt
KlmJan skrev:det är det jag itne fattar. Hur i hela världen går man tillväga för att skriva om en rekursiv formel till en aritmetisk formel? Det hade gjort hela uppgiften 100 gånger enklare.
Deluppgiften inna nvar med en aritmetisk formel och den löste jag busenkelt
Jag tänkte typ att första termen är 4, och då märker jag att skillnaden är konstant mellan termerna i den rekursiva talföljden. Det är ju definitionen av en aritmetisk talföljd, att termernas skillnader är konstant! Så då tänkte jag, okej nu borde f(n) = 4 + 11(n-1) funka?
KlmJan skrev:det är det jag itne fattar. Hur i hela världen går man tillväga för att skriva om en rekursiv formel till en aritmetisk formel? Det hade gjort hela uppgiften 100 gånger enklare.
Deluppgiften inna nvar med en aritmetisk formel och den löste jag busenkelt
Tänk på att formeln säger "lägg till 11 till det förra talet för att få det nya talet". Då kan man också säga, "lägg till 22 från det förrförra talet för att få det nya talet". Eller om man tar det några steg till, "lägg till för att gå från det första talet till det :te talet".
Nu förstår jag. Tack för hjälpen!
