asymptot

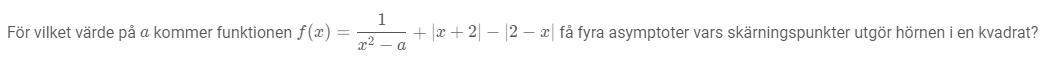
Ser att ingen svarat på denna. Och jag får erkänna att jag inte kan ge så mycket hjälp heller.

När x går mot oändligheten går f(x) – 2x mot noll, dvs y = 2x är en asymptot oavsett a.

När x går mot minus oändl går f(x) + 2x mot noll dvs y = –2x är en asymptot  oavsett a.

När x går mot +a eller –a så går f(x) mot + eller – oändligheten, dvs x = a och x = –a är asymptoter. 

Detta ger möjligen fem skärningspunkter mellan asymptoter, (a, 2a), (a, –2a), (–a, 2a), (–a, –2a) samt (0, 0). De fyra först nämnda är hörn i en rektangel med sidor 2a och 4a. Sedan har vi origo, men jag ser inte att den punkten hjälper. Sorry.

|x+2| - |2-x| går faktiskt mot 4, eller t o m är 4, när x är stort.

Jag får det till att det finns två asymptoter (med värden) oavsett a.

$y=\pm 4$

Tillägg: 22 dec 2022 15:56

En vidare tanke är att man alltid kommer få två vertikala asymptoter på formen $x=\pm \sqrt{a}$.

Tillägg: 22 dec 2022 16:00

Här är mitt lösningsförslag :). Tror det blir rätt.

Ja! Ursäkta mina vimsigheter, de lodräta asym är ju ±Roten ur a.

Och absolutbeloppen hade jag också rört till. Inga snälla barn här när tomten kommer.