Avtagande giftkoncentration
 Hej! Jag förstår inte vad jag gjort för fel här...
Hej! Jag förstår inte vad jag gjort för fel här...
Kanske har jag räknat ut k fel? Vet inte om jag har gjort rätt där eftersom jag tog skillnaden mellan mängden vid 20 timmar och 28 timmar delat med 8.
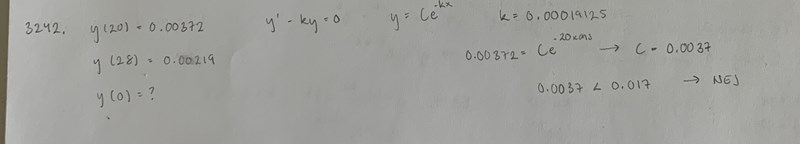
Svaret är att den högsta koncentrationen Kalle fick i sig var 0,014
Differentialekvationen y'=-ky, k>0, med villkor y(0)=0.00372 och y(8)=0.00219 ger att y(t)=0.00372 e^(-0.06623 t). BEstäm y(-20).
Hej,
Sättet du kom fram till k var nog fel. Du verkar ha tagit dY/dT för tiden 28 och 20.
Du vet y(20) och y(28). C är konstant. k är okänd.
Ställ upp
y(20)=C*e^(-k*20)
y(28)=C*e^(-k*28)
Två ekvationer, två okända (C och k). Sen får du lösa ut k (med hjälp av potensregler och ln för att bli av med e). Sen avslutar du precis som du gjort i sista steget! Fast med rätt k-värde :)
Gjorde på detta vis och fick fram en koncentration på 0.014!
Du ansätter att eftersom så bör y kunna skrivas på formen .
Detta håller jag med om. Låt oss därför mha. våra kända värden räkna ut de okända variablerna C och k.
Om man dividerar de två uttrycken med varandra så får man ut
Från detta uttryck kan man räkna ut k, och sedan stoppa in i de två första uttrycken för att få ut C.
Jag förstår in riktigt din utträkning men jag tror att du missade att man kunde utföra divisionen ovan för att komma vidare.



