Baser och vektorer
"Bestäm a+b samt a-b när och "
Jag förstår inte riktigt hur jag ska förstå det här med baser. Går det att rita/visualisera på något förståeligt sätt?
Baserna kan också kallas enhetsvektorer. Den enklaste vektorn (utom nollvektorn) är ju vektorn med längden 1 och som är parallell med en av axklarna. Om du vill ha en vektor som går längs x-axeln så kan du helt enkelt multiplicera x-enhetsvektorn med ett tal. Tex ex*3 ger en vektor som är tre lång och parallell med xaxeln. e1 och e2 har jag inte sett förrut men de menar ex och ey
Ja, du kan rita i godtycklig riktning och sedan i en annan godtycklig riktning. När du tar a+b så tar du helt enkelt 1st från a och 4st från b och lägger ihop. Samma med . Tänkt att du byter ut e1 och e2 mot x och y. Det blir samma sak.
Qetsiyah skrev:Baserna kan också kallas enhetsvektorer. Den enklaste vektorn (utom nollvektorn) är ju vektorn med längden 1 och som är parallell med en av axklarna. Om du vill ha en vektor som går längs x-axeln så kan du helt enkelt multiplicera x-enhetsvektorn med ett tal. Tex ex*3 ger en vektor som är tre lång och parallell med xaxeln. e1 och e2 har jag inte sett förrut men de menar ex och ey
Tack!
emilg skrev:Ja, du kan rita i godtycklig riktning och sedan i en annan godtycklig riktning. När du tar a+b så tar du helt enkelt 1st från a och 4st från b och lägger ihop. Samma med . Tänkt att du byter ut e1 och e2 mot x och y. Det blir samma sak.
Tack!
Qetsiyah skrev:e1 och e2 har jag inte sett förrut men de menar ex och ey
Då hade de nog skrivit det ;) Med e1 och e2 menas två godtyckliga basvektorer. De behöver inte vara ortogonala t.ex.
emilg skrev:Ja, du kan rita i godtycklig riktning och sedan i en annan godtycklig riktning. När du tar a+b så tar du helt enkelt 1st från a och 4st från b och lägger ihop. Samma med . Tänkt att du byter ut e1 och e2 mot x och y. Det blir samma sak.
Du nämnde att och kan ritas i en godtycklig riktning, men då borde väl inte svaret för a+b samt a-b bli samma som om man ritar dem längs x-axeln (1;0) samt y-axeln (0;6). Eller tänker jag helt fel? Svaret på a+b ska bli (5;1) men då har de väl utgått från att baserna är ritade mot x-axeln och y-axeln?
Jag bifogar en bild. Basbegreppet är ett mycket centralt moment i linjär algebra.
Låt och vara två icke-parallella vektorer i planet.
I figuren noterar vi att .
Vi utnyttjar därmed det faktum, att de röda vektorerna är parallella med resp. .
Vidare: Vektorerna och utgör en bas i planet.
I uttrycket är koordinaterna för a med avseende på basen .
Anm Basen är ortogonal om basvektorerna är inbördes ortogonala.
Är dessutom basvektorernas längder lika med 1, har vi en
ortonormerad bas eller en ON-bas. Detta gäller i nedanstående figur.
Analogt resonerar vi för vektorn b, som på koordinatform skrivs , eller hur?
Nu är det en enkel sak att beräkna a+b resp. a-b. Överens?

abcdefg skrev:emilg skrev:Ja, du kan rita i godtycklig riktning och sedan i en annan godtycklig riktning. När du tar a+b så tar du helt enkelt 1st från a och 4st från b och lägger ihop. Samma med . Tänkt att du byter ut e1 och e2 mot x och y. Det blir samma sak.
Du nämnde att och kan ritas i en godtycklig riktning, men då borde väl inte svaret för a+b samt a-b bli samma som om man ritar dem längs x-axeln (1;0) samt y-axeln (0;6). Eller tänker jag helt fel? Svaret på a+b ska bli (5;1) men då har de väl utgått från att baserna är ritade mot x-axeln och y-axeln?
Prova att rita ett koordinatsystem där e1 är "två rutor åt höger" och e2 är "en ruta åt höger och tre rutor uppåt". Rita in vektorerna och dels i detta koordinatsystem, dels i ett vanligt ortonormerat koordinatsystem. Lägg upp bilderna här. Ser de likadana ut?
Smaragdalena skrev:abcdefg skrev:emilg skrev:Ja, du kan rita i godtycklig riktning och sedan i en annan godtycklig riktning. När du tar a+b så tar du helt enkelt 1st från a och 4st från b och lägger ihop. Samma med . Tänkt att du byter ut e1 och e2 mot x och y. Det blir samma sak.
Du nämnde att och kan ritas i en godtycklig riktning, men då borde väl inte svaret för a+b samt a-b bli samma som om man ritar dem längs x-axeln (1;0) samt y-axeln (0;6). Eller tänker jag helt fel? Svaret på a+b ska bli (5;1) men då har de väl utgått från att baserna är ritade mot x-axeln och y-axeln?
Prova att rita ett koordinatsystem där e1 är "två rutor åt höger" och e2 är "en ruta åt höger och tre rutor uppåt". Rita in vektorerna och dels i detta koordinatsystem, dels i ett vanligt ortonormerat koordinatsystem. Lägg upp bilderna här. Ser de likadana ut?
Okej, jag testade att rita och så som du beskrev (a fick tyvärr inte plats i koordinatsystemet). Skulle jag då kunna säga att både (3;23) och (5;1) är en lösning till a+b?
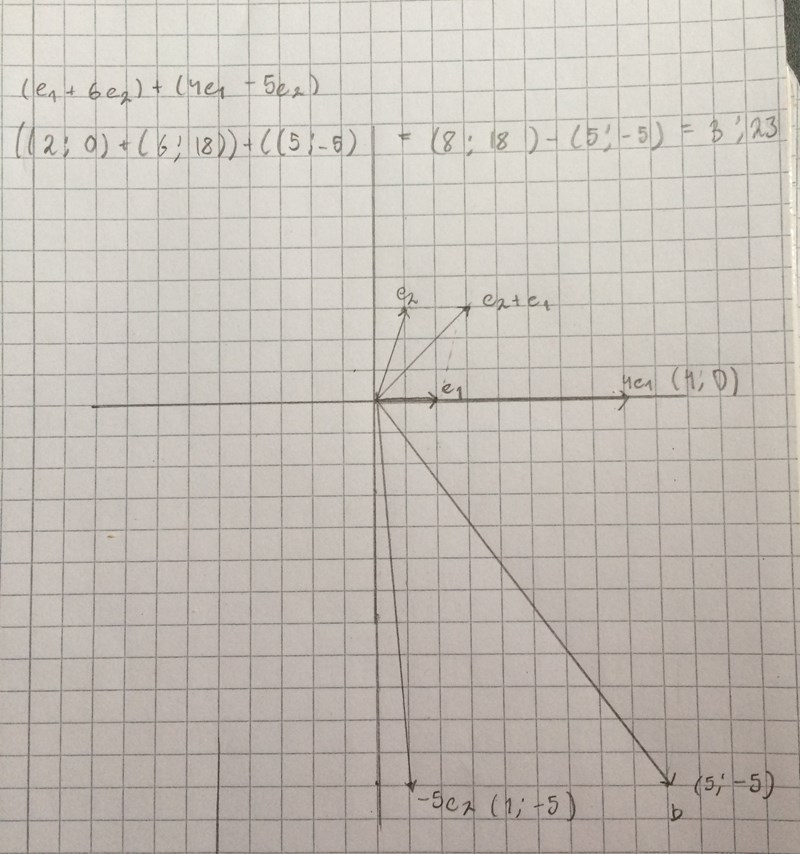
Jag vet tyvärr inte vad ett ortonormerat koordinatsystem är, det är inget vi gått igenom ännu.
abcdefg skrev:Smaragdalena skrev:abcdefg skrev:emilg skrev:Ja, du kan rita i godtycklig riktning och sedan i en annan godtycklig riktning. När du tar a+b så tar du helt enkelt 1st från a och 4st från b och lägger ihop. Samma med . Tänkt att du byter ut e1 och e2 mot x och y. Det blir samma sak.
Du nämnde att och kan ritas i en godtycklig riktning, men då borde väl inte svaret för a+b samt a-b bli samma som om man ritar dem längs x-axeln (1;0) samt y-axeln (0;6). Eller tänker jag helt fel? Svaret på a+b ska bli (5;1) men då har de väl utgått från att baserna är ritade mot x-axeln och y-axeln?
Prova att rita ett koordinatsystem där e1 är "två rutor åt höger" och e2 är "en ruta åt höger och tre rutor uppåt". Rita in vektorerna och dels i detta koordinatsystem, dels i ett vanligt ortonormerat koordinatsystem. Lägg upp bilderna här. Ser de likadana ut?
Okej, jag testade att rita och så som du beskrev (a fick tyvärr inte plats i koordinatsystemet). Skulle jag då kunna säga att både (3;23) och (5;1) är en lösning till a+b?
Jag vet tyvärr inte vad ett ortonormerat koordinatsystem är, det är inget vi gått igenom ännu.
Jag förstår verkligen inte vad din bild har att göra med det som jag bad dig att rita. Du har ritat ut vektorn e1+e2 rätt, men det var inte med i uppgiften.
Ett ortogonalt koordinatsystem är ett koordinatsystem där basvektorerna är ortogonala, d v s vinkelräta mot varandra, och normerade, d v s basvektorerna har längden 1 - d v s ett alldeles vanligt koordinatsystem som man lärde sig redan på grundskolan. Nu när du är på universitetet behöver du lämna alla förutfattade meningar, som att det är självklart att basvektorerna är vinkelräta mot varandra och att de är lika långa.
Försök igen att rita så som jag beskrev! Gör först ett rutnät med skeva rutor (det underliggande rutiga pappret underlättar), rita ut vektorn , rita ut vektorn , rita ut vektorn , rita ut vektorn , lägg in bilden här.
emilg skrev:Qetsiyah skrev:e1 och e2 har jag inte sett förrut men de menar ex och ey
Då hade de nog skrivit det ;) Med e1 och e2 menas två godtyckliga basvektorer. De behöver inte vara ortogonala t.ex.
Så pass? Kan då vilka vektrorer som helst som inte är linjärt beroende vara baser och spänna upp nåt område?
Qetsiyah skrev:emilg skrev:Qetsiyah skrev:e1 och e2 har jag inte sett förrut men de menar ex och ey
Då hade de nog skrivit det ;) Med e1 och e2 menas två godtyckliga basvektorer. De behöver inte vara ortogonala t.ex.
Så pass? Kan då vilka vektrorer som helst som inte är linjärt beroende vara baser och spänna upp nåt område?
I ett tvådimensionellt vektorrum är två linjärt oberoende vektorer alltid en bas för vektorrummet.
PATENTERAMERA skrev:Qetsiyah skrev:emilg skrev:Qetsiyah skrev:e1 och e2 har jag inte sett förrut men de menar ex och ey
Då hade de nog skrivit det ;) Med e1 och e2 menas två godtyckliga basvektorer. De behöver inte vara ortogonala t.ex.
Så pass? Kan då vilka vektrorer som helst som inte är linjärt beroende vara baser och spänna upp nåt område?
I ett tvådimensionellt vektorrum är två linjärt oberoende vektorer alltid en bas för vektorrummet.
Så gäller samma för R^n om vi har n linjärt oberoende vektorer?
Ja?
Qetsiyah skrev:PATENTERAMERA skrev:Qetsiyah skrev:emilg skrev:Qetsiyah skrev:e1 och e2 har jag inte sett förrut men de menar ex och ey
Då hade de nog skrivit det ;) Med e1 och e2 menas två godtyckliga basvektorer. De behöver inte vara ortogonala t.ex.
Så pass? Kan då vilka vektrorer som helst som inte är linjärt beroende vara baser och spänna upp nåt område?
I ett tvådimensionellt vektorrum är två linjärt oberoende vektorer alltid en bas för vektorrummet.
Så gäller samma för R^n om vi har n linjärt oberoende vektorer?
Ja?
Ja det gäller generellt för n-dimensionella vektorrum ().
Qetsiyah skrev:emilg skrev:Qetsiyah skrev:e1 och e2 har jag inte sett förrut men de menar ex och ey
Då hade de nog skrivit det ;) Med e1 och e2 menas två godtyckliga basvektorer. De behöver inte vara ortogonala t.ex.
Så pass? Kan då vilka vektrorer som helst som inte är linjärt beroende vara baser och spänna upp nåt område?
Två vektorer, vilka som helst, bara de inte är nollvektorer och de inte är parallella, kan spänna upp planet. De behöver inte vara vinkelräta. De behöver inte vara lika långa.
dr_lund skrev:Jag bifogar en bild. Basbegreppet är ett mycket centralt moment i linjär algebra.
Låt och vara två icke-parallella vektorer i planet.
I figuren noterar vi att .
Vi utnyttjar därmed det faktum, att de röda vektorerna är parallella med resp. .
Vidare: Vektorerna och utgör en bas i planet.
I uttrycket är koordinaterna för a med avseende på basen .
Anm Basen är ortogonal om basvektorerna är inbördes ortogonala.
Är dessutom basvektorernas längder lika med 1, har vi en
ortonormerad bas eller en ON-bas. Detta gäller i nedanstående figur.Analogt resonerar vi för vektorn b, som på koordinatform skrivs , eller hur?
Nu är det en enkel sak att beräkna a+b resp. a-b. Överens?
Tack för bra förklaring! Dock är jag fortfarande inte med på varför , som är parallell med ,motsvarar x-koordinaten och , som är parallell med , motsvarar y-koordinaten. Kan det inte vara tvärtom? Om så är fallet, blir inte svaret annorlunda då? (Är något trögfattad när det kommer till detta område)
Som du ser av min figur har jag medvetet valt ett "vanligt rätvinkligt koordinatsystem" där x-axeln har som riktningsvektor, och motsvarande för y-axeln. Notera också att jag medvetet har valt enhetslängd på basvektorerna, dvs
. Hoppas detta är svar på din fundering.




