Behöver hjälp i en uppgift där jag behöver använda derivatans definition!
Derivera f (x) = 1/(2x+1) med hjälp av derivatans definition.
Det jag har gjort:
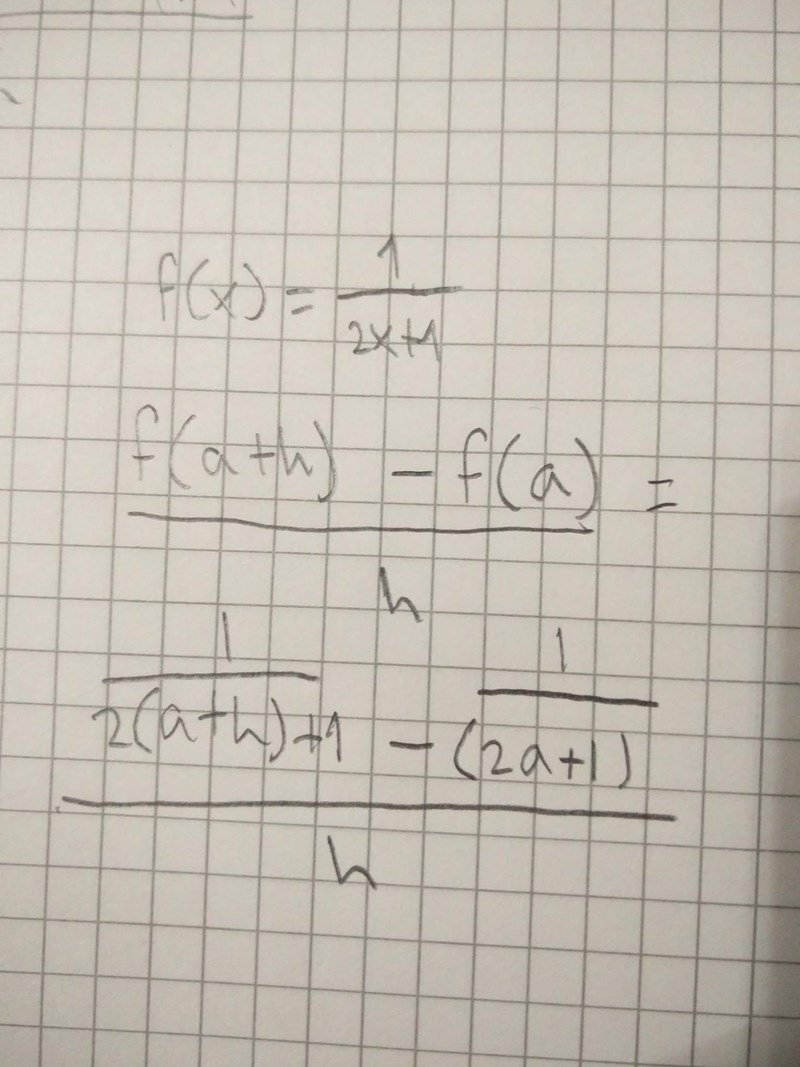
Svaret ska bli: f'(x) -2/(2x+a)^2
uppskattar all hjälp jag kan få
Vad är a?
Prova att göra bråken liknämniga och förenkla.
Om du tittar i en formelsamling så kommer du se att derivatans definition har två olika formler. En med x och en med a.
krock-odilen skrev :Om du tittar i en formelsamling så kommer du se att derivatans definition har två olika formler. En med x och en med a.
Två olika formler? Det låter osannolikt.
Jaja, utnyttja att gemensamt bråkstreck så kommer du antagligen kunna förenkla utefter det.
olika är nog fel men det står (f(a+h) - f(a))/h är lika med (f(x) - f(a))/x-a
krock-odilen skrev :olika är nog fel men det står (f(a+h) - f(a))/h är lika med (f(x) - f(a))/x-a
Man skriver derivatans definition i punkten som .
Det går också att skriva om den (rita så kan du nog härleda det) som .
Notera att i första men i andra, två olika saker! (men geometriskt likadana kan man säga)Glöm inte limes när du skriver formler, det gör mycket! :)
Tack för att du klargjorde det för mig!
Uppgiften kvarstår, jag försökte att förenkla och fick svaret till 2 vilket är fel...
krock-odilen skrev :Tack för att du klargjorde det för mig!
Uppgiften kvarstår, jag försökte att förenkla och fick svaret till 2 vilket är fel...
Okej.
Du har alltså ?
Kan du posta en bild på hur du förenklade så kan jag se var du gjort fel. :-)
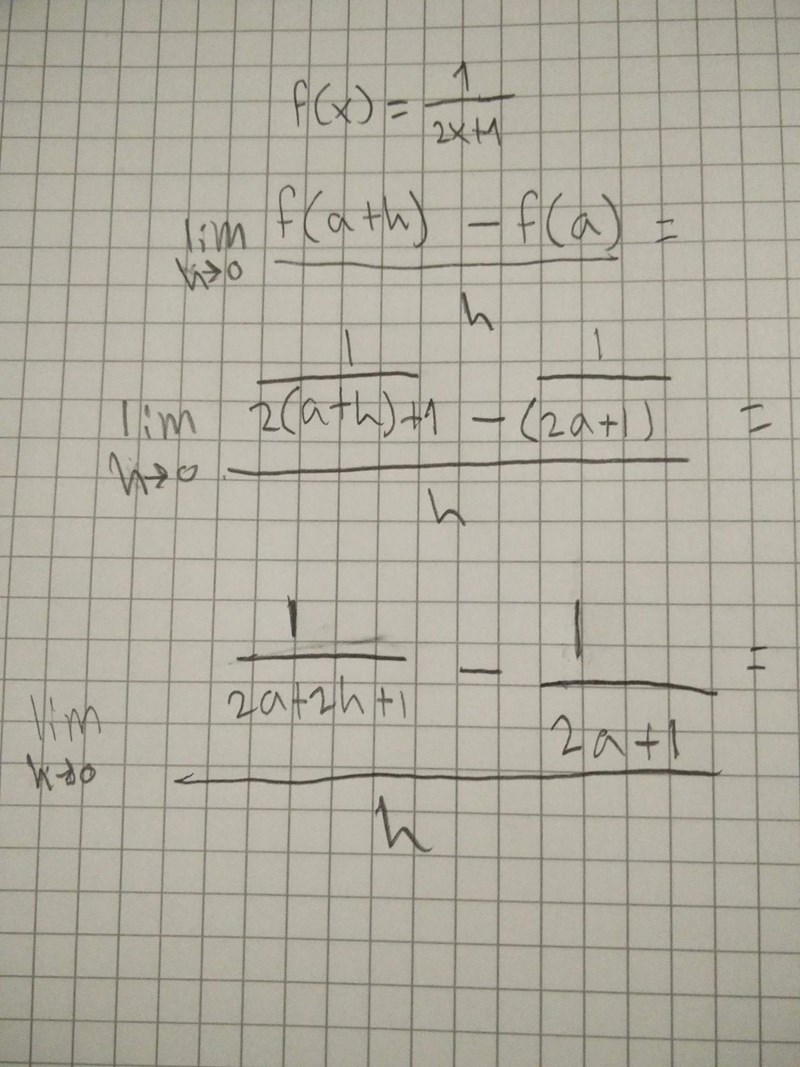 Längre än så här kommer jag inte.
Längre än så här kommer jag inte.
Testa multiplicera med nämnaren för och vice versa för . Förenkla sedan täljaren och (om du kan) förkorta bort h. :)
ska jag multiplicera nämnarna med de förenklade nämnaren eller?
Om vi t.ex tar den första nämnaren "2(x+h)+1" ska jag förenkla den först och sedan multiplicera med den andra nämnaren "2x+1"?
Ja, det verkar bra. Du kan antingen förenkla först och multiplicera sedan, eller multiplicera först och förenkla sedan. Jag skulle förenkla först. Du kommer att kunna förenkla bort en del termer när du har skrivit på gemensamt bråkstreck.
Men om jag har två bråk som har samma nämnare och täljare så bör differensen bli 0.
Jag har multiplicerat nämnarna med varandra och har förenklat men vet inte hur jag ska fortsätta. Ska jag fortsätta med att förenkla h:na genom att dividera med h?
Det kanske var otydligt skrivet tidigare, du skall inte bara multiplicera nämnarna med varandra utan förlänga det första bråket med det andra bråkets nämnare och förlänga det andra bråket med det första bråkets nämnare.
Du får inte två bråk som har samma täljare och nämnare (hade du fått det så hade differensen varit 0). Du bör ha fått fram två täljare där några termer tar ut varandra.
Visa hur du har gjort, så är det lättare att hjälpa till.
Ja, jag klurade faktiskt ut det och fick rätt svar. Tack så jättemycket! Uppskattar verkligen all hjälp jag har fått <3



