Beräkna förändringen i entropi i en gasfylld låda

Halloj!

Jag håller på att studera exempeluppgiften nedan

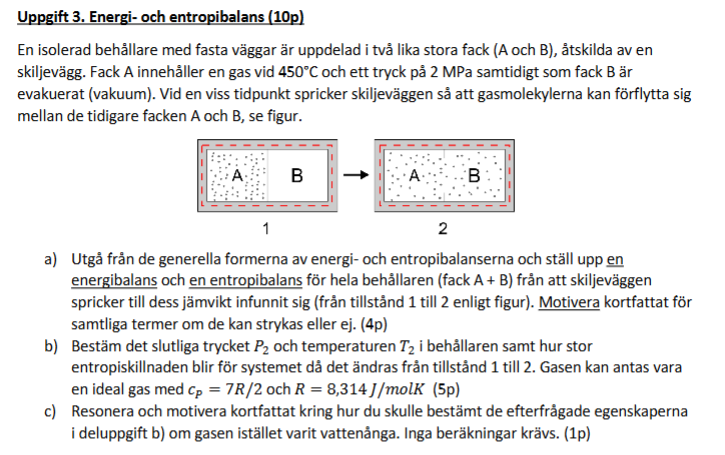
Specifikt håller jag på att studera uppgift (b). Eftersom en ideal gas följer sambandet $U\left(T\right)=cNRT$ och vi vet att den sammanlagda, interna energin är fixerad under hela transformationen $1\to 2$ vet vi att $T_1 = T_2 = 450\;^\circ\mathrm{C}$ . Enligt sambandet $PV=NRT$ vet vi dessutom att trycket halveras då volymen tvåfaldigas. Med andra ord har vi $P_2=1\;\mathrm{MPa}$ . Nu gäller det att bestämma entropiskillnaden och det är här jag har lite problem.

För ett system som detta kan vi anta att entropin är en funktion av intern energi, volym och substansmängd. Vi har alltså $S=S\left(U,V,N\right)$ . Dessutom vet vi att entropin är additiv över $A$ och $B$ och vi har:

$\displaystyle dS=\frac{\partial S_A }{\partial U_A}dU_A+\frac{\partial S_A}{\partial V_A}dV_A+\frac{\partial S_A}{\partial N_A}dN_A+\frac{\partial S_B }{\partial U_B}dU_B+\frac{\partial S_B}{\partial V_B}dV_B+\frac{\partial S_B}{\partial N_B}dN_B$

Eftersom systemet är isolerat måste $dU_A = -dU_B$ och likaså $dN_A=-dN_B$ Volymdifferentialerna är noll eftersom väggen som separerar $A$ och $B$ är orörlig. Detta ger:

$\displaystyle dS=\left(\frac{1}{T_A}-\frac{1}{T_B}\right)dU_A+\left(\frac{\mu_B}{T_B}-\frac{\mu_A}{T_A}\right)dN_A$

Vi kan använda tillståndsekvationerna för en ideal gas för att hitta uttryck för $dU_A$ samt $dN_A$ :

$\displaystyle dU_A=cR\left(TdN_A+N_AdT_A\right)$

Vad gäller $dN_A$ blir det lite mer mödosamt men ändå inte omöjligt:

$\displaystyle dN_A=d\left(\frac{P_AV_A}{RT_A}\right)=\frac{RT_Ad\left(P_AV_A\right)-P_AV_Ad\left(RT_A\right)}{\left(RT_A\right)^2}=\frac{V_AT_AdP_A-V_AP_AdT_A}{RT_A^2}$

Om vi substituerar in detta i vårt uttryck har vi:

$\displaystyle dS=\left(\frac{1}{T_A}-\frac{1}{T_B}\right)cR\left(TdN_A+N_AdT_A\right)+\left(\frac{\mu_B}{T_B}-\frac{\mu_A}{T_A}\right)\frac{V_AT_AdP_A-V_AP_AdT_A}{RT_A^2}$

Detta känns extremt krånligt även om det säkert hade gått att lösa så här. Det stora problemet är ju att de kemiska potentialerna finns med i uttrycken vilket gör att integrering inte riktigt blir helt straight forward. Dessutom blir det väl krångligt att integrera t.ex. $1/T_B$ med avseende på $T_A$ och $dN_A$ eftersom $T_B$ ?. Men det kanske är ett problem eftersom man alltid kan skriva om $dT_A$ i termer av $dT_B$ och $dN_A$ i termer av $dN_B$ då man delar upp integralen. Hur ska man tänka här?

Kan man kanske tänka så här istället?

Under rimliga antaganden har vi $U=U(S,V,N)$ . För att beräkna entropiskillnaden mellan två jämviktstillstånd kan vi föreställa oss en fiktiv, kvasistatisk process som förbinder jämviktstillstånden. Överallt under en sådan process gäller då

$\displaystyle dU=\frac{\partial U}{\partial S}dS+\frac{\partial U}{\partial V}dV=TdS-PdV$

Eftersom $dU=0$ överallt under processen eftersom systemet är isolerat kommer vi fram till att

$\displaystyle dS=\frac{PdV}{T}=\frac{NR}{V}dV$

Så integrering ger

$\displaystyle \Delta S=\int_{V_1}^{V_2}\frac{NR}{V}dV=NR\ln\frac{V_2}{V_1}$

Med vetskapen att $V_2=2V_1$ får vi att den molära entropiförändringen är

$\displaystyle \Delta s= R\ln2\approx 5.\! 76\;\mathrm{Jmol^{-1}K^{-1}}$

Tycker ni att det ser ut som ett korrekt resonemang? Det jag tycker är märkligt är att värmekapaciteten vid konstant tryck aldrig användes, men de har ju angivit denna för att den behövs, eller...?

Lustigt nog stötte jag just på ett exempel i Callen's Thermodynamics där Callen diskuterar exakt det jag gjorde i #3 (vilket gav rätt svar). Nedan följer en skärmdump

Här blir man ju faktiskt lite rädd. Callen verkar tycka att det problematiskt att $dS>0$ medan $dQ=0$ så att $dQ\ne TdS$ , varför han menar att denna process inte borde inordnas som kvasistatisk. Men jag förstår inte riktigt vad problemet med detta är. Varför skulle $dQ=TdS$ för alla kvasistatiska processer? Kvasistatisk innebär ju bara att systemet är i jämvikt under hela processen (mer tekniskt att den följer en kontinuerlig kurva i sitt konfigurationsrum) och det gör ju uppenbarligen den här processen (per antagande). Är det inte snarare så att $dQ=TdS$ kanske helt enkelt inte gäller för alla kvasistatiska processer? Om det är meningen att expansionen från $V$ till $V+dV$ ska ske instantant (alltså inte kvasistatiskt) gäller ju knappast $dS=(NR/V) dV$ ...

Bumpar.

Jag diskuterade detta med några väldigt kunniga fysiker och det verkar som om Callen helt enkelt gjorde ett misstag här. Det finns ingenting i hans definition (vilket är den gängse definitionen i den termodynamiska litteraturen) som säger att $dQ=TdS$ för alla kvasistatiska processer. Han var väl lite trött eller något, helt enkelt...

Spännande😅

Visst är det?! Ett bra skäl att studera sin analys, visst? :-)

Svara

Visa senaste svar