Beräkna Fourierserie i L^2(-4,4) i en punkt

Hej!

Jag sitter med quizuppgiften nedan:

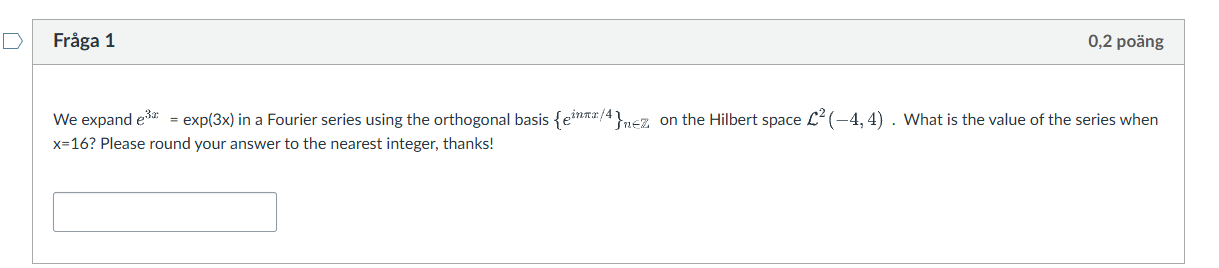
Jag har använt den vanliga formen av Fourierserien:

$\displaystyle e^{3x}=\sum_{n\in\mathbb{Z}} \frac{\left\langle e^{3x},e^{i\pi nx/4} \right\rangle}{||e^{i\pi nx/4}||^2}e^{i\pi nx/4}$

Efter lite uträkning kom jag fram till att i $\mathcal{L}^{\;2}(-4,4)$ :

$\displaystyle e^{3x}=\sum_{n\in\mathbb{Z}} \frac{\left\langle e^{3x},e^{i\pi nx/4} \right\rangle}{||e^{i\pi nx/4}||^2}e^{i\pi nx/4}= \frac{e^{12-i\pi n}-e^{i\pi n-12}}{24-2i\pi n}\sum_{n\in\mathbb{Z}}e^{in\pi x/4}$

Nu är mitt problem att jag inte vet vad summan till höger konvergerar till i $x=16$ . Hur ska man komma fram till det?

Dessutom har jag två frågor:

Vad är det egentligen jag har räknat ut? Är det den "8-periodiska" utvidgningen till funktionen som definieras av $f\left(x\right)=e^{3x}$ på något intervall?
Vad krävs egentligen för att en funktion ska vara periodisk? Vår föreläsare insisterar på att en funktion är $p$ -periodisk om $f(x+p)=f(x)$ för alla $x\in \mathrm{dom}f$ , men räcker det verkligen? Borde vi inte också kräva att $f^\prime(x+p)=f^\prime(x)$ ? Det verkar ju konstigt att t.ex. sinus skulle vara $\pi$ -periodisk istället för $2\pi$ -periodisk...

Som frågan är formulerad, så behöver man inte alls ta fram fourierserien. Man vill bara veta vad seriens summa blir.

Notera också att fourierkoefficienter som innehåller $n$ måste stå innanför summan, d.v.s. de kan inte brytas ut ur summan.

Jag har inte kontrollräknat, men om du räknat skalärprodukterna rätt, så har du hittat en fourierserie till den 8-periodiska utvidgningen, d.v.s. till funktionen

$f(x)=\left\{ \begin{array}{cl} e^{3x} & \text{då } x \in (-4, 4)\\\text{periodisk utvidg.}& \text{då } x \notin [-4,4] \end{array}\right.$

Basfunktionerna $e^{in\pi x/4}$ har den gemensamma grundperioden 8, så serien är 8-periodisk. Om $S(x)$ betecknar seriens summa, så gäller att $S(x) = S(x+8) = S(x+16)$ o.s.v. I synnerhet är $S(16) = S(8) = S(0) \stackrel{(!)}{=} f(0) = e^{3\cdot 0} = 1$ .

Om funktionen är styckvis deriverbar (vilket den 8-periodiska utvidgningen av exp(3x) är), så är fourierseriens summa lika med ursprungsfunktionen i alla kontinuitetspunkter. Eftersom $f$ är kontinuerlig i punkten $x=0$ , så är $S(0)=f(0)$

Funktionen kallas för $p$ -periodisk om $f(x+p) = f(x)$ gäller för alla $x \in D_f$ . Det är det enda kravet för $p$ -periodiciteten. Genom att derivera båda leden i detta samband, så inser man att sambandet i sig implicerar att $f^\prime(x+p) = f^\prime(x)$ för alla $x \in \text{Int}(D_f)$ . Därmed finns det inget behov att ställa upp ett extra krav på att derivatan skall vara periodisk.

Förstår inte riktigt vad du menar med att "sinus skulle vara $\pi$ -periodisk". Den är inte det. $\sin(x+\pi) = \sin x$ gäller endast i ett fåtal punkter $x \in \mathbb{R}$ . Periodicitet kräver att sambandet gäller alla $x\in\mathbb{R}$ .

Tack för svar!

Jag råkade formatera fel med summan.

Jag tänkte fel angående periodicitet med sinus.

Jag tror att jag är med på resonemanget. Så istället för att ta fram serien inser man att funktionen är 8 periodisk och eftersom vi då har S(16)=S(0), och vi vet att serien inom [-4,4] bara är e^3x, så vet vi att S(0)=f(0)=1?

Ja, exakt.

Man borde dock motivera varför summan konvergerar punktvis till ursprungsfunktionen, t.ex. genom att nämna (styckvis) deriverbarhet.

(Eftersom $f \in L^2(-4,4)$ , så gäller att $S = f$ i $L^2$ -meningen, vilket i sin tur medför att $S(x) = f(x)$ för nästan alla $x \in (-4,4)$ . "Nästan alla" innebär att det kan finnas en undantagsmängd med lebesguemåttet 0. Att likheten $S(x) = f(x)$ faktiskt gäller alla $x \in (-4,4)$ behöver motiveras med lämpliga konvergenssatser/inversionssatser/ "fundamental theorem of Fourier series".)

Svara

Visa senaste svar