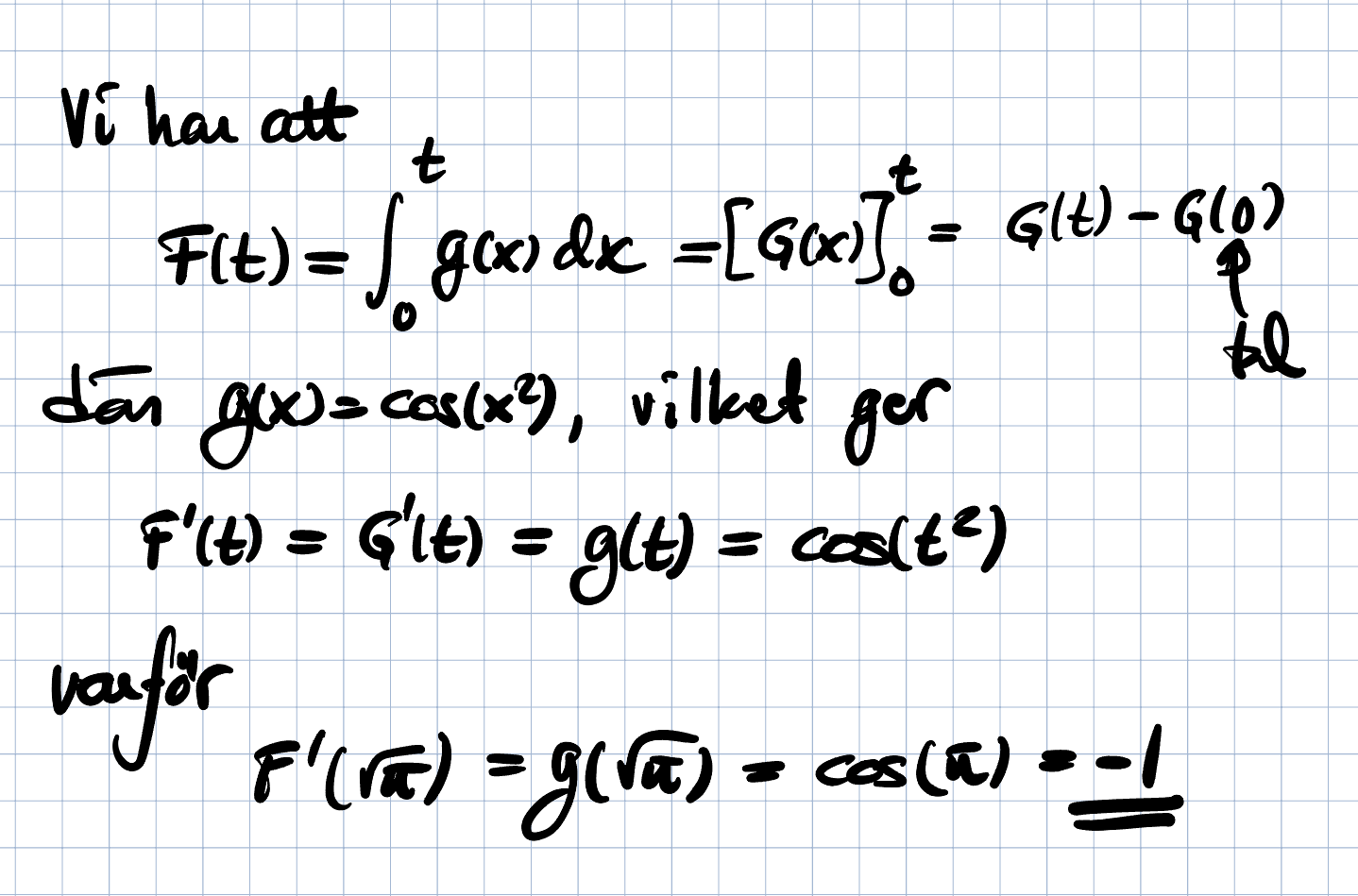Beräkna integral cos(x^2) (Matematik/Matte 4/Integraler och tillämpningar)

Yes, då lyckades jag komma fram till rätt svar ändå. Tänkte att det var för enkelt och det måste ligga något krångligare bakom eller så..

Tack

Du har dock rätt gällande antiderivatan till $\cos (x^2)$ . Det finns självfallet en funktion som har $\cos(x^2)$ som derivata, MEN den kan inte skrivas som en ändlig kombination av ”vanliga” funktioner (polynom, exponentialfunktioner, trigonometriska funktioner, deras inverser, etc). Funktioner som har dessa typer av antiderivator sägs ha en icke-elementär antiderivata.

Några andra exempel är

$\dfrac{\sin(x)}x$

$e^{\cos x}$

$e^{-x^2}$ (klassikern)

$\dfrac{\ln(1-x)}x$

$\dfrac{\arctan(x)}x$ .

Tillägg: 3 aug 2025 23:55

Vill bara utveckla att man självklart fortfarande kan jobba med funktioner som är "icke-elementära". Exempelvis kan man använda att $\displaystyle \ln\left(1-x\right) = -\frac x - \frac{x^2}2 - \frac{x^3}3 + \dots$ . Sedan kan man dividera med $x$ och ta antiderivatan av varje term. Detta ger en oändlig serie som representerar funktionen vars derivata är $\frac{\ln(1-x)}x$ . Denna funktion har faktiskt massvis med trevliga egenskaper och ett speciellt namn (dilogarithm). Det är den enda speciella funktionen (och dess generaliseringar) jag själv spenderat mycket tid på. Mycket trevlig funktion!

Det är lustigt att du tar upp begreppet elementär funktion för det var något jag tänkte på imorse. Finns det någon allmänt accepterad definition av "elementär funktion"? Hela begreppet har alltid verkat lite mystiskt för mig.

naytte skrev:
Det är lustigt att du tar upp begreppet elementär funktion för det var något jag tänkte på imorse. Finns det någon allmänt accepterad definition av "elementär funktion"? Hela begreppet har alltid verkat lite mystiskt för mig.

Jag vet inte exakt, jag tror det finns någon definition.

Själv tycket jag också det är lite luddigt. Man skulle kunna börja med att tänka (informellt och heuristiskt här) att elementära funktioner är funktioner ändliga ”applikationer” av de fyra räknesätten och deras ”förlängningar” (igen, luddigt, för att få med exempelvis irrationella exponenter) och respektive funktions invers. Intuitivt tänker jag att det får med allt förutom trigonometriska funktioner. De kanske man kan anse är ”vanliga nog”?

Dock är detta jag nyss skrev inte särskilt bra och rätt påhittat. Det finns ju andra funktioner som inte är ”elementära” och kan definieras på liknande sätt till trigonometriska funktioner, exempelvis dessa

Tillägg: 3 aug 2025 21:49

Jag sitter just nu på ett tåg med dålig uppkoppling, så jag har inte riktigt lust att söka runt på detta just nu (kollar på nedladdade serier på Netflix istället!).

Det är dock ett mycket intressant ämne, särskilt med tanke på att det finns satser om kriterier på vilka funktioner som kan ha icke-elementära antiderivator (tror Liouville har någon sådan sats döpt efter sig? Om jag kommer ihåg rätt?). Därmed måste det väl finnas en exakt definition?

Detta svar på MathSE verkar ha en rätt bra definition av elementära funktioner. Jag har dock inte hittat någon definition från en mer konkret källa, jag tycker wikipedia är lika luddig som jag var tidigare i tråden:

"In mathematics, elementary functions are those functions that are most commonly encountered by beginners [...]"

Frågan jag har är hur mycket man ens behöver tänka på gällande om en funktion är "elementär" eller inte. Har dessa elementära funktioner några egenskaper som vissa icke-elementära funktioner saknar?

Tillägg: 4 aug 2025 00:09

Det var också ett annat svar på samma MathSE tråd som länkade till en artikel som kanske svarar på våra frågor, jag är lite trött och vill inte läsa den ikväll dock.

Jag hade redan kollat igenom det första svaret på MathSE som du länkade men det finns en stor oklarhet med detta. Hur ska man definiera t.ex. $|x|$ , som enligt inläggsskaparen själv är en elementär funktion? Jag tänkte att man kunde notera att $x\mapsto \log x^2$ är elementär, och då är även $x\mapsto \exp(\frac{1}{2}\log x^2)$ elementär.

Problemet är att denna funktion inte har samma domän som $|x|$ eftersom $\log 0$ är odefinierat.

Hmm, det är sant. Ett annat sätt att, i alla fall, halvt definiera $|x|$ är via:

$\displaystyle \left|x\right| = \arccos\left(\cos x\right) = \frac\pi 2 + i \log\left(\sqrt{1-\cos^2 x}+i\cos x\right)=\frac\pi 2 + i \log\left(\exp\left(\frac 12\log\left(1-\cos^2 x\right)\right)+i\cos x\right)$

Samma problem uppstår såklart här, då detta endast stämmer för $x \in (-\pi, \pi)\textbackslash\{0\}$ enligt våra definitioner.

Om man skulle addera till definitionerna att det är ok att "fylla i" removable discontinuities (känner inte till namnet på svenska) så skulle problemet med $|x|$ vara löst med din definition. Däremot måste man då dra in gränsvärden.

Tillägg: 6 aug 2025 01:07

Frågan är dock, är $|x|$ ens en elementär funktion? Enligt trådskaparen är det det, men är det normalt att ha den med? Från det följer det ju att alla polygona funktioner* är elementära, stämmer det? (Man kan skriva alla polygona funktioner som en ändlig summa av absolutbelopp och linjära funktioner)

* En kontinuerlig funktion $g(x)$ definierad över ett intervall $[a,b]$ är polygon om det existerar en ändlig, ökande talföljd $a=x_0 < x_1 <\dots < x_n = b$ där $g(x)$ är linjär över varje delintervall $[x_{i-1},x_i]$ där $i=1,\dots n$ .

Ett annat ord skulle väl kunna vara "piecewise linear function" (som också är kontinuerlig på hela dess domän)

Varför skulle man behöva gränsvärden för att ta bort diskontinuiteten i $x=0$ ? Om vi tillåter oss en styckvis definition (vilket borde vara tillåtet?) borde vi kunna göra så här:

$\displaystyle x\mapsto\left\{\begin{array}{ll}\exp\left(\frac{1}{2}\ln x^2\right), & x\ne0 \\ 0, & x=0\end{array}\right.$

Egentligen borde vi kunna göra så här varje gång det finns ett ändligt antal hål i funktionen. Det känns lite konstigt att en elementär funktion skulle vara styckvis definierad men samtidigt handlar ju det mer om vårt symbolspråk för funktioner än någon egenskap hos funktionen i sig...

Tillägg: 6 aug 2025 02:08

Och ja, om absolutvärdesfunktionen är elementär tror jag att alla polygona funktioner måste vara det också!

Min tanke med att man behöver gränsvärden är om man specifikt ska "fylla i" diskontinuiteter. Mest tänkte jag att en "removable discontinuity" definieras med gränsvärden (att gränsvärdet från vänster och höger är lika fast funktionens värde inte är det). Om man tillåter styckvis definitioner helt och hållet är det självklart inga problem.

Däremot, om man tillåter styckvis definitioner kan man ju även konstruera en massa exotiska funktioner. Vad skulle vi säga om exempelvis Dirichlet's funktion eller Thomae's funktion? Även om dessa funktioner är välkända kanske det inte är det första man tänker på som en elementär funktion.