Beräkning av gränsvärde mha. Taylorpolynom
Hej! Jag skrev en kontroversiell envariabelstentamen på KTH nyligen (80% kuggade) och upptäckte att jag fått 0p på den första frågan. Det är lite brist på kommentarer odyl. i det rättade tentabladet, så jag förstår inte vad jag gjorde fel.
Man ska då bestämma gränsvärdet till denna: 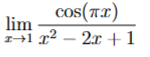 Efter att ha läst facit har jag insett att det finns ett enklare sätt man kan lösa det på (analysera funktionen och konstatera att nämnaren , och täljaren , och att allting därför måste gå mot ) men jag bestämde mig för att utnyttja Taylorpolynom under tentan, då detta är en metod vi lärt oss.
Efter att ha läst facit har jag insett att det finns ett enklare sätt man kan lösa det på (analysera funktionen och konstatera att nämnaren , och täljaren , och att allting därför måste gå mot ) men jag bestämde mig för att utnyttja Taylorpolynom under tentan, då detta är en metod vi lärt oss.
Andra gradens Taylorpolynom av runt punkten x = 1 är T(x) = +
Så jag fick att gränsvärdet ovan då är detsamma som .
Om man då utvecklar gränsvärdet:
Och så fick jag ut mitt svar. är då rätt svar, men min lösning måste ha varit så fel att den inte ens kunde ge tröstpoäng. Tänker jag fel kring taylorpolynom i gränsvärden? Någon som ser vart det blir tokigt?
Och detta var då facits lösning:
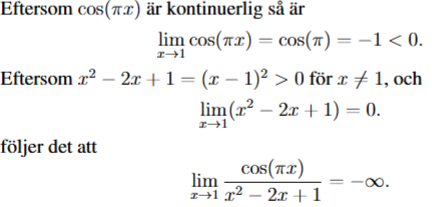
Uppskattar alla svar!
Har inte kollat jättenoga men det ska inte vara några konstigheter att använda Taylorserier. Jag ser inget fel med din lösning, även om den inte är den "snyggaste" metoden i detta fall. Jag skulle klaga till examinatorn, eller åtminstone be om en förklaring.
Uppgiften handlar om oegentliga gränsvärden. Dessa får ej betraktas som gränsvärden i vanlig mening. Till exempel gäller inte de "vanliga" reglerna
(om
Tvärtom gäller de bara då och . De är alltså inte tillämpliga här!
Oftast undviker man -beteckningen i samband med oegentliga gränsvärden. Istället formulerar man regler som
då , om och , då .
Och det är uppenbart en sådan regel man alluderar till i facit. Förvisso kan man visa att
om och
Men man får inte slå isär "gränsvärden", varken som termer eller som täljare/nämnare, utan att bevisa det. Fullt poängavdrag låter dock lite hårt.
Jag kanske är helt ute och cyklar nu, men borde man inte på något sätt kunna visa att det är okej att dela upp oändliga gränsvärden på samma sätt som vi delar upp ändliga gränsvärden?
Man borde väl kunna trixa lite med den här något modifierade varianten av gränsvärdets definition:
naytte skrev:Jag kanske är helt ute och cyklar nu, men borde man inte på något sätt kunna visa att det är okej att dela upp oändliga gränsvärden på samma sätt som vi delar upp ändliga gränsvärden?
Man borde väl kunna trixa lite med den här något modifierade varianten av gränsvärdets definition:
Jag tror 'poängen' i #3 är att (x->oo)
0 = lim(0) = lim(x-x) =/= lim(x)-lim(x)=oo-oo,
ty det är inte sant att oo-oo = 0.
Men om h(x) = f(x) + g(x), samt och , så måste det gälla att . Bevis: trivialt.
Så beviset med Taylor-utveckling måste väl vara formellt korrekt.
Blev det noll poäng för svaret? Konstigt i så fall.
PATENTERAMERA skrev:Men om h(x) = f(x) + g(x), samt och , så måste det gälla att . Bevis: trivialt.
Så beviset med Taylor-utveckling måste väl vara formellt korrekt.
Blev det noll poäng för svaret? Konstigt i så fall.
Jag håller med, det går väl utmärkt att använda gränsvärdeslagarna för att visa att gränsvärden inte existerar. Eller så missar jag något. Det man gör då formellt sett är att anta att gränsvärdet existerar och utnyttjar t.ex. den regel du skrivit, som följer direkt från den vanliga regeln om summor. Om man då når en motsägelse betyder det att gränsvärdet inte existerar.
För just och gäller som sagt
Skulle dock inte påstå att det är _helt_ trivialt att visa, jag har rättat tillräckligt många tentor och inlämningsuppgifter för att veta att en ansenlig mängd studenter blandar ihop det så fort ett epsilon-delta är inblandat eller om man måste anpassa sin triangelolikhet.
Om vi tittar på den något mer intressanta regeln
Så förstår vi snart att "en motsägelse" ställer ganska omfattande krav på vår definition av motsägelse. Vi kan ju med relativt enkla val av och då skapa situationer som
(eller något annat godtyckligt tal)
saknar både gränsvärde och oegentligt gränsvärde.
Men i fallet c skilt från 0 och g kontinuerlig x0 måste g(x) vara skilt från 0 i en omgivning till x0 Då måste vi väl rimligen få ett oegentligt gränsvärde?
Jag mejlade examinatorn och frågade. Han sa att det jag skrivit såg korrekt ut, så nu har jag skickat in en begäran om betygsomprövning. Jag planerar att skriva den kommande omtentan i kursen så det vore skönt att reda ut eventuella frågetecken
D4NIEL skrev:För just och gäller som sagt
Skulle dock inte påstå att det är _helt_ trivialt att visa, jag har rättat tillräckligt många tentor och inlämningsuppgifter för att veta att en ansenlig mängd studenter blandar ihop det så fort ett epsilon-delta är inblandat eller om man måste anpassa sin triangelolikhet.
Om vi tittar på den något mer intressanta regeln
Så förstår vi snart att "en motsägelse" ställer ganska omfattande krav på vår definition av motsägelse. Vi kan ju med relativt enkla val av och då skapa situationer som
(eller något annat godtyckligt tal)
saknar både gränsvärde och oegentligt gränsvärde.
Lagen gäller även när ett av gränsvärdena är oändligheten, så länge , alltså så länge vi inte har något på den obestämda formen . Så det går utmärkt att använda även då.




