Berg- och dalbana

tan 10° kan det knappast bli.

Här är en gammal tråd om det: https://www.pluggakuten.se/trad/redovisningsuppgift-berg-och-dalbanan

Hej,

I en lösningen såg jag att det stod att:

(y= ax^2+px+q=a(x+p^2/2a)^2-((p^2)/4a)+q= a(x-b)^2+c

Där b= -p/2a och c= -p^2/4a+q)

Kan ni förklara till mig hur de fick fram b och c från ingenstans?

Det står i uppgiften att de tre delarna av berg-och-dalbanan kan skrivas som tre stycken andragradsfunktioner, och ALLA andragradsfunktioner kan skrivas som f(x) = ax²+px+q, eller som f(x) = k(x-x₁)(x-x₂) eller f(x) = a(x-b)²+c. 

Här föredrar man det tredje skrivsättet, och räknar om det första så att det blir det tredje. Du har ju skrivit på rad 2 nerifrån hur man har tagit fram b och c.

När jag ville skriva om det första det vill säga f(x) = ax2+px+q till det tredje dvs f(x) = a(x-b)2+c så fick jag att det blir a(x-p)^2+c vilket ger a(x^2-2px+p^2)+c. Jag fick inte fram a(x+p^2/2a)^2-((p^2)/4a)+q

Visa steg för steg hur du har gjort så kan vi hjälpa dig att hitta var det har blivit fel. Använd formelskrivaren för att skriva lösliga formler, eller skriv på ett papper och ladda upp bilden.

är du fortfarande här?

Ghais Ismail skrev:

är du fortfarande här?

Ja, men jag kan inte läsa det du har skrivit, jag blir så här:

Ghais Ismail, jag vet inte om du bryter mot regeln att man skall vänta åtminstone 24 timmar innan man bumpar din tråd eller att man inte får skriva tjat-inlägg eller båda två. Läs reglerna, de finns i högerspalten! /moderator

Och jag tycker lika illa om tjat-inlägg specifikt riktade till mig som tjat-PM.

Här är det omvänt:

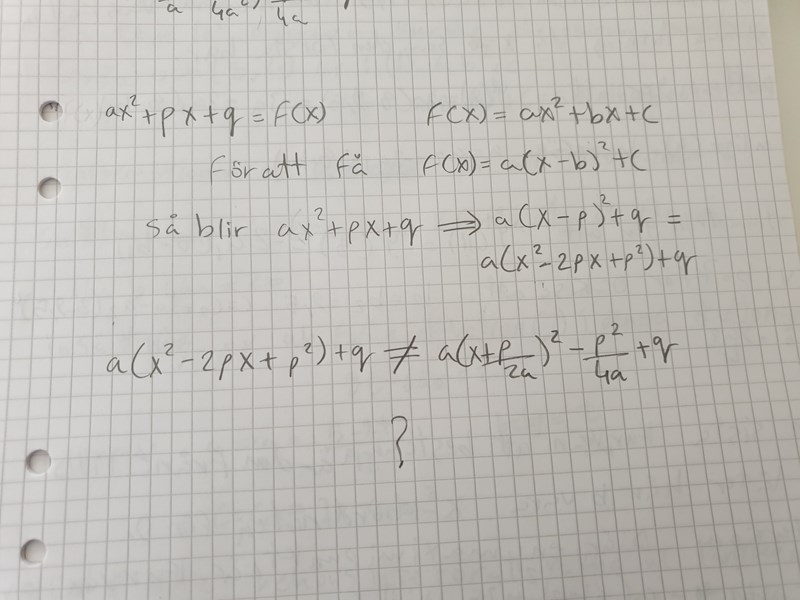
Jag ber om ursäkt för mitt respektlösa beteende :)

Skyll dig själv. Det är förhoppningsvis någon annan som vill hjälpa dig.

Snälla jag behöver din hjälp, jag visste inte om reglerna här. Jag ber om ursäkt igen. 

Hej.

Jag har beskrivit hur jag skulle försöka lösa uppgiften i den här tråden.

Kolla igenom den och försök använda tipsen du får där.

Jag kom fram till detta men har faktiskt ingen aning om de jag gjorde var rätt. Jag vet inte heller vad nästa steg kommer bli

EDIT - lade till alternativ för positiv/negativ lutning.

En derivata anges inte i grader.

Rita en figur av en rätvinklig triangel där kateterna är parallella med koordinataxlarna och vinkeln till vänster är 10°.

Du ser då att tan(10°) = $\frac{\Delta y}{\Delta x}$, vilket innebär att derivatan i punken A har värdet tan(10°) om lutningen är positiv och -tan(10°) om lutningen är negativ.

Aha, när jag ville räkna ut CD så fick jag detta. Vet du vad steget som kommer därefter är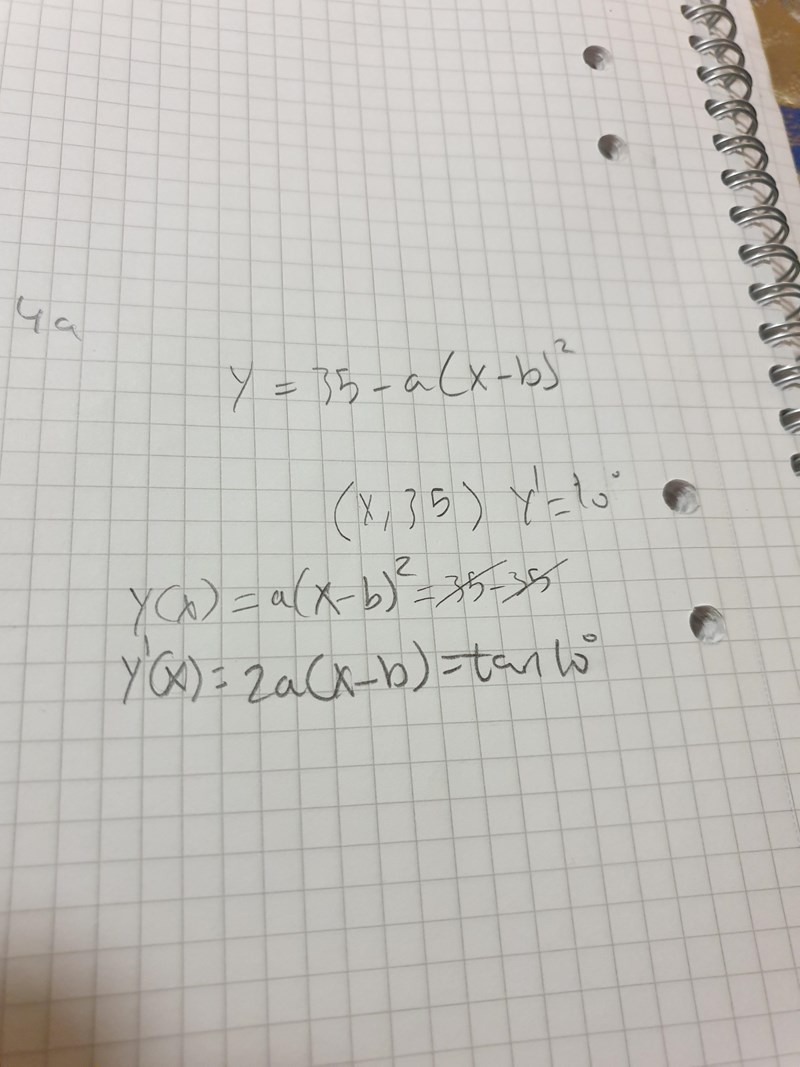

Det hör en bild till uppgiften, kan du ladda upp den?

Där framgår det vilken x-koordinat punkt A har och huruvida lutningen 10° avser en uppförs- eller nerförsbacke.

Jag hänger inte med på din lösning.

Tänker du att det ska finnas ett enda funktionsuttryck $f(x)$ som ska gälla för hela sektionen från A till D?

Här är en länk på en annan tråd som har bilden: https://www.pluggakuten.se/trad/redovisningsuppgift-berg-och-dalbanan/

På samma länk kan du se hur personen har kommit fram till sista steget det vill säga att räkna längden på deljurvan CD. Den förra infogade bilden visar funktionen som man ska använda sig av enligt den infogade tråden. Så jag undrar om du kan hjälpa mig till nästa steg tack :)

Enligt bilden är lutningen vid A negativ, vilket inte stämmer med den uträkning som är gjord i andra tråden.

Frågan är om du hänger med på uträkningarna.

Skulle du kunna göra om dem själv?

T.ex. med de beteckningar jag har givit i den tråd jag länkade till tidigare, dvs $f_1, f_2, f_3, a_1, a_2, a_3$ osv?

Jag tänker att eftersom det är en inlämningsuppgift så bör du skriva en egen lösning.

Jag gjorde klart allting förutom den sista delen då man räknar längden på delkurvorna. Ni använde er av en formel i en annan länk http://www2.maths.lth.se/query/faq/bana.pdf Om du kollar sista sidan ser du att dem använt sig aven integral men vart får dem själva funktionen under rotenur tecknet? Har dem ens använt sig av primitiva??? Tack

Är det 1, 2, 3, 4 eller något annat du vill få förklarat?

Det är punkt 2

Båglängd

Det står inte mycket om detta i mina gymnasieböcker, men det här hittade jag i min matte4-bok. Det säger ju egentligen mindre, men kanske kan avdramatisera det hela?

Djupare förståelse kan man få i högskolematte i böcker om envariabelanalys och engelsk litteratur typ "Calculus"

Här kommer en länk till hur man beräknar kurvlängd. LÄNK