Bestäm arean av den yta so uppkommer då kurvan y= 2sqrt(x) roteras kring y-axeln

Zeptuz skrev:

Bestäm arean av den yta so uppkommer då kurvan $y =2\sqrt{x}$, 0<=x<=1 roteras ett varv kring y-axeln

mina uträkningar: $$\begin{gathered} 2\mathrm{\pi }{\int }_0^1\mathrm{x}\sqrt{1+{\left(\frac{1}{\sqrt{\mathrm{x}}}\right)}^2}d\mathrm{x}= 2\mathrm{\pi }{\int }_0^1\mathrm{x}\sqrt{\mathrm{x}+\frac{1}{\mathrm{x}}}\mathrm{dx} =2\mathrm{\pi }{\int }_0^1\sqrt{{\mathrm{x}}^2(1+\frac{1}{\mathrm{x}})}\mathrm{dx}= \\ =2\mathrm{\pi }{\int }_0^1\sqrt{{\mathrm{x}}^2+\mathrm{x}}\mathrm{dx} \end{gathered}$$

Jag vet inte riktigt hur jag ska integrera härifrån. Jag har testat att substituera $u = x^2+x och u = \sqrt{x^2+x}$men det blir inte rätt. Hur ska jag integrera den här integralen?

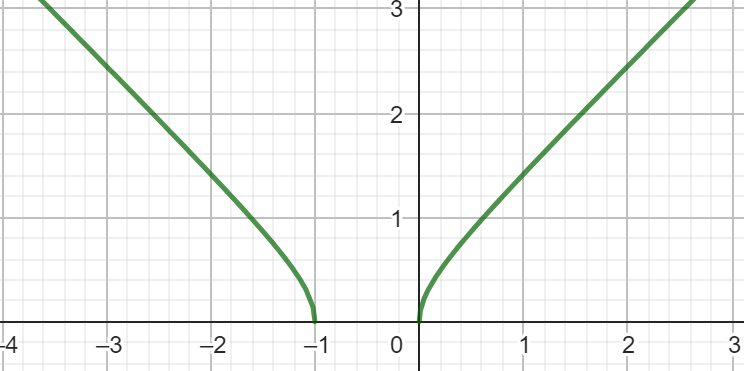
Som vanligt: Börja med att rita. Lägg upp bilden här. 

För att lösa integralen kan du testa att göra variabelbytet $\displaystyle x=\tan^2{\theta}$. Finns det någon trevlig identitet du då kan utnyttja? :)

Tillägg: 24 dec 2023 01:37

Nu när jag börjar lösa integralen på detta sätt blir det ganska komplicerat. Men det går. Men det lär finnas ett bättre sätt!

naytte skrev:

För att lösa integralen kan du testa att göra variabelbytet $\displaystyle x=\tan^2{\theta}$. Finns det någon trevlig identitet du då kan utnyttja? :)

Tips om du fastnar

Börja med att plocka fram ett uttryck för $\displaystyle \mathrm{d}x$. Det blir då: 

$\displaystyle \mathrm{d}x=2\tan{\theta}\cdot \sec^2{\theta} \cdot \mathrm{d}\theta$

Substituera sedan in detta i integralen:

$\displaystyle \int_{}^{}\sqrt{x(x+1)}\mathrm{d}x=\int_{}^{}\sqrt{\tan^2\theta(\tan^2\theta+1)}\cdot2\tan\theta\cdot \sec^2\theta \mathrm{d}\theta$

Ser du någon fin identitet här?

---

Tillägg: 24 dec 2023 01:37

Nu när jag börjar lösa integralen på detta sätt blir det ganska komplicerat. Men det går. Men det lär finnas ett bättre sätt!

Ja jag har sett den lösningsvägen också, men vår lärare använder inte den här typen av konvertering och jag har nästan ingen kunskap om sekantfunktionen så jag  håller mig till det läraren har lärt oss. Men tack ändå!

Smaragdalena skrev:

Zeptuz skrev:

Bestäm arean av den yta so uppkommer då kurvan $y =2\sqrt{x}$, 0<=x<=1 roteras ett varv kring y-axeln

mina uträkningar: $$\begin{gathered} 2\mathrm{\pi }{\int }_0^1\mathrm{x}\sqrt{1+{\left(\frac{1}{\sqrt{\mathrm{x}}}\right)}^2}d\mathrm{x}= 2\mathrm{\pi }{\int }_0^1\mathrm{x}\sqrt{\mathrm{x}+\frac{1}{\mathrm{x}}}\mathrm{dx} =2\mathrm{\pi }{\int }_0^1\sqrt{{\mathrm{x}}^2(1+\frac{1}{\mathrm{x}})}\mathrm{dx}= \\ =2\mathrm{\pi }{\int }_0^1\sqrt{{\mathrm{x}}^2+\mathrm{x}}\mathrm{dx} \end{gathered}$$

Jag vet inte riktigt hur jag ska integrera härifrån. Jag har testat att substituera $u = x^2+x och u = \sqrt{x^2+x}$men det blir inte rätt. Hur ska jag integrera den här integralen?

Som vanligt: Börja med att rita. Lägg upp bilden här. 

_{Zeptuz skrev:}

Ja jag har sett den lösningsvägen också, men vår lärare använder inte den här typen av konvertering och jag har nästan ingen kunskap om sekantfunktionen så jag  håller mig till det läraren har lärt oss. Men tack ändå!

Förstår. Jag är lite osäker på hur man skulle lösa detta utan trig-sub, en u-sub verkar lite suspekt här. Eller jag kan åtminstone inte hitta någon bra sådan. Men sekansfunktionen är inte så konstig egentligen, det gäller helt enkelt att:

$\displaystyle \sec x = \frac{1}{\cos x}$

Har du en bild på frågan? 

oneplusone2 skrev:

Har du en bild på frågan? 

 

Frågan är exakt det jag skrev. Bara en text som skriver det där.

OK låt oss utgå ifrån att området som definieras av $y=2\sqrt{x}$och 0<x<1 ska roteras runt y axeln.

Cylinderformeln

$$\begin{gathered} V={\int }_0^{1}2*\pi *x*h\left(x\right)dx \\ V=2\pi {\int }_0^{1}xh\left(x\right)dx=2\pi {\int }_0^{1}x2\sqrt{x}dx=4\pi {\int }_0^{1}x\sqrt{x}dx \\ V=4\pi {\int }_0^1{x}^{3/2}dx =4\pi {\left[\frac{x^{5/2}}{5/2}\right]}_0^1=\frac{8\pi }{5} \end{gathered}$$

Är du inte bekant med cylinderformeln kan du köra skivformeln i y-led

$$\begin{gathered} y=2\sqrt{x} \\ x=\frac{y^2}{4} \\ 0<x<1 \Rightarrow 0<y<2 \\ {V}_y={\int }_0^2\pi *r^2 dy =\pi {\int }_0^2\frac{y^4}{16}dy=\frac{\pi }{16}{\int }_0^2{y}^{4}dy \\ {V}_y=\frac{\pi }{16}{\left[\frac{y^5}{5}\right]}_0^2=\frac{32\pi }{80}=\frac{2\pi }{5} \end{gathered}$$
$V_y$ska subtraheras från en större cylinder med dimensionerna r=1 h=2

$$\begin{gathered} V=V_c-V_y \\ {V}_c=\pi r^2*h=\pi *1*2=2\pi \\ V=V_c-V_y=2\pi -\frac{2\pi }{5}=\frac{8\pi }{5} \end{gathered}$$

Är det AREAN du är ute efter så blir det andra beräkningar.

oneplusone2 skrev:

OK låt oss utgå ifrån att området som definieras av $y=2\sqrt{x}$och 0<x<1 ska roteras runt y axeln.

Cylinderformeln

$$\begin{gathered} V={\int }_0^{1}2*\pi *x*h\left(x\right)dx \\ V=2\pi {\int }_0^{1}xh\left(x\right)dx=2\pi {\int }_0^{1}x2\sqrt{x}dx=4\pi {\int }_0^{1}x\sqrt{x}dx \\ V=4\pi {\int }_0^1{x}^{3/2}dx =4\pi {\left[\frac{x^{5/2}}{5/2}\right]}_0^1=\frac{8\pi }{5} \end{gathered}$$

Är du inte bekant med cylinderformeln kan du köra skivformeln i y-led

$$\begin{gathered} y=2\sqrt{x} \\ x=\frac{y^2}{4} \\ 0<x<1 \Rightarrow 0<y<2 \\ {V}_y={\int }_0^2\pi *r^2 dy =\pi {\int }_0^2\frac{y^4}{16}dy=\frac{\pi }{16}{\int }_0^2{y}^{4}dy \\ {V}_y=\frac{\pi }{16}{\left[\frac{y^5}{5}\right]}_0^2=\frac{32\pi }{80}=\frac{2\pi }{5} \end{gathered}$$
$V_y$ska subtraheras från en större cylinder med dimensionerna r=1 h=2

$$\begin{gathered} V=V_c-V_y \\ {V}_c=\pi r^2*h=\pi *1*2=2\pi \\ V=V_c-V_y=2\pi -\frac{2\pi }{5}=\frac{8\pi }{5} \end{gathered}$$

Är det AREAN du är ute efter så blir det andra beräkningar.

hmm svaret enligt facit är $\frac{\mathrm{\pi }(6\sqrt{2}-\ln (3+2\sqrt{2}\left)\right)}{4}$, är det här samma?

oneplusone2 skrev:

OK låt oss utgå ifrån att området som definieras av $y=2\sqrt{x}$och 0<x<1 ska roteras runt y axeln.

Cylinderformeln

$$\begin{gathered} V={\int }_0^{1}2*\pi *x*h\left(x\right)dx \\ V=2\pi {\int }_0^{1}xh\left(x\right)dx=2\pi {\int }_0^{1}x2\sqrt{x}dx=4\pi {\int }_0^{1}x\sqrt{x}dx \\ V=4\pi {\int }_0^1{x}^{3/2}dx =4\pi {\left[\frac{x^{5/2}}{5/2}\right]}_0^1=\frac{8\pi }{5} \end{gathered}$$

Är du inte bekant med cylinderformeln kan du köra skivformeln i y-led

$$\begin{gathered} y=2\sqrt{x} \\ x=\frac{y^2}{4} \\ 0<x<1 \Rightarrow 0<y<2 \\ {V}_y={\int }_0^2\pi *r^2 dy =\pi {\int }_0^2\frac{y^4}{16}dy=\frac{\pi }{16}{\int }_0^2{y}^{4}dy \\ {V}_y=\frac{\pi }{16}{\left[\frac{y^5}{5}\right]}_0^2=\frac{32\pi }{80}=\frac{2\pi }{5} \end{gathered}$$
$V_y$ska subtraheras från en större cylinder med dimensionerna r=1 h=2

$$\begin{gathered} V=V_c-V_y \\ {V}_c=\pi r^2*h=\pi *1*2=2\pi \\ V=V_c-V_y=2\pi -\frac{2\pi }{5}=\frac{8\pi }{5} \end{gathered}$$

Är det AREAN du är ute efter så blir det andra beräkningar.

Ja, det står ju i frågan att det gäller arean.

Jag utgår nu ifrån att din integral faktiskt motsvarar arean, och tog mig friheten att lösa den med metoden jag föreslog förut, eftersom inga framsteg verkar ha gjorts sedan dess:

Jag gjorde helt enkelt om integralen så att istället för att integrationsgränserna går från 0 till 1 (för x) går de nu från 0 till pi/4 (för theta). Hoppas det hjälpte!

Man kan kvadratkomplettera x²+x så att det blir (x + 1/2)² - 1/4. Om man sedan sätter t = x + 1/2 har man $\sqrt{t^2 - 1/4}$ och har kommit en bit på väg.