Bestäm det minsta uttrycket för P

Jag tolkar det så här:

Du kan nog helt enkelt lösa integralen och minimera funktionen denna definierar (något på formen $y=f(p)$) genom att hitta extrempunkter.

jag förstår inte riktigt hur du menar

Jag menar att du ska "beräkna" integralen. Är du med på att du då kommer få något uttryck som definierar en funktion?

ja, eller när jag integrar en funktion som kommer det åka i grad tal

Ja, det händer om du integrerar ett polynomuttryck. Men i vårt fall måste vi först jobba lite med uttrycket. Försök lösa integralen och visa ditt försök här!

Jag jag inte det i #2 ?

Inlägget hade inte dykt upp för mig av någon skum anledning..!

Det är en bestämd integral. Sätt in integrationsgränserna x=1 (det har du inte gjort) respektive x=0 (det har du gjort) i den funna primitiva funktionen

Så ska kjag toppa in x=1 och x=0 i det här uttrycket ?

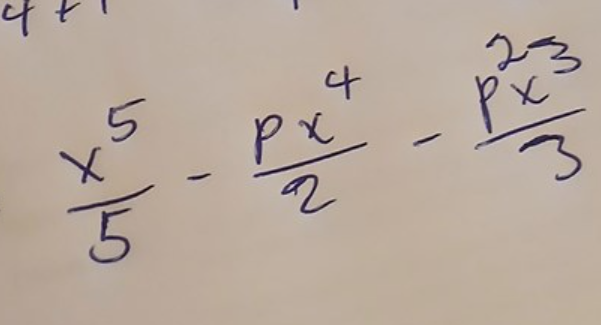
Ja.

På så sätt får du ett uttryck som bara har variabeln $p$ kvar och då kan du hitta dess minimum

Btw. det finns ett teckenfel alldeles i början.

$(x^2 - px)^2 = x^4 - 2px^3 + p^2 x^2$

Lägg märke till att det är plustecknet i sista termen p.g.a. kvadreringsformeln $(a-b)^2 = a^2-2ab+b^2$

slarvfel, jag undrar för att hitta dess minimum kan jag ta andra derivatan av uttrycket som fick i  # 11 ?

Arup skrev:

slarvfel, jag undrar för att hitta dess minimum kan jag ta andra derivatan av uttrycket som fick i  # 11 ?

Nja, uttrycket i svar #11 är inte rätt.

Dels är det ett teckenfel framför sista termen, dels har du bara tagit fram en primitiv funktion, inte beräknat själva integralen genom att sätta in gränserna x = 0 och x = 1.

Om du gör det så kommer du att få fram ett abdragradsuttryck där den obekanta storheten är p.

När du sedan ska bestämma detta uttrycks minsta värde så kan du använda olika metoder.

En av dessa är att hitta den stationära punkten genom att derivera med avseende på den obekanta storheten p och sedan sätta förstaderivatan lika med 0. Eftersom det är ett andragradsuttryck så "vet" du om detta ger dig minimi- eller maximipunkten.

Om du ändå vill visa det algebraiskt så kan du, precis som du antyder, ta fram andraderivatan (med avseende på p) och se om den är positiv vid den stationära punkten.

Jag förstår inte riktigt skillnaden mellan den primitiva funktionen och integralen. Vad är skillnaden ?

När du beräknar en integral tar du först fram en primitiv funktion för integranden, sedan sätter du in övre respektive undre gränsen och förenklar.

Exempel

$\int_{a}^{b}f(x)\operatorname dx=F(b)-F(a)$

Här är $F(x)$ en primitiv funktion till $f(x)$ och $F(b)-F(a)$ är den beräknade integralen.

Jag får det det till så här 

Nej, eftersom $F(x)=\frac{x^5}{5}-\frac{px^4}{2}+p^2x^2$ så är

$F(1)=\frac{1^5}{5}-\frac{p\cdot1^4}{2}+p^2\cdot1^2=\frac{1}{5}-\frac{p}{2}+p^2$ och

$F(0)=\frac{0^5}{5}-\frac{p\cdot0^4}{2}+p^2\cdot0^2=0$

oj vad dum jag är

man glömmer lätt ibland

Arup skrev:

oj vad dum jag är

Nej det är du inte alls.

Alla går vilse ibland. Och det är lite lurigt att det först är x och sedan p som är den intressanta obekanta storheten

Yngve skrev:

Arup skrev:

slarvfel, jag undrar för att hitta dess minimum kan jag ta andra derivatan av uttrycket som fick i  # 11 ?

Nja, uttrycket i svar #11 är inte rätt.

Dels är det ett teckenfel framför sista termen, dels har du bara tagit fram en primitiv funktion, inte beräknat själva integralen genom att sätta in gränserna x = 0 och x = 1.

Om du gör det så kommer du att få fram ett abdragradsuttryck där den obekanta storheten är p.

När du sedan ska bestämma detta uttrycks minsta värde så kan du använda olika metoder.

En av dessa är att hitta den stationära punkten genom att derivera med avseende på den obekanta storheten p och sedan sätta förstaderivatan lika med 0. Eftersom det är ett andragradsuttryck så "vet" du om detta ger dig minimi- eller maximipunkten.

Om du ändå vill visa det algebraiskt så kan du, precis som du antyder, ta fram andraderivatan (med avseende på p) och se om den är positiv vid den stationära punkten.

Är det så här ?

Jag vet att här det tecken fel, men det påverkar väl inte lösningen.

Du är inte klar ännu.

Ditt andragradsuttryck är p²/3-p/2+1/5.

Uppgiften gällar att bestämma det värde på p som minimerar detta uttryck.

Vad kommer du fram till?

Pröva sedan gärna samma uträkning utan teckenfelet och se vad du kommer fram till då.

Kan jag använda på formeln eller skulle jag stoppa in 2/3 i ursprungs ekvationen dvs (x^2-px)^2 ?

Jag tror att du blandar ihop det lite.

Vi tar ett påhittat enkelt exempel som visar tillvägagångssättet tydligare.

Säg att du har en andragradsfunktion g(t) = t²-t-2 och att uppgiften gäller att bestämma vilket värde på t som minimerar detta uttryck.

Det finns flera olika sätt att göra detta.

Metod 1 - symmetrilinje

Ett sätt är att utnyttja att eftersom g(t) är en andragradsfunktion så ligger det minsta eller största) värdet på symmetrilinjen.

Symmetrilinjen ligger mitt emellan nollställena. Pq-formeln ger att nollställena är t = -1 och t = 2.

Symmetrilinjen är därför t = 1/2.

Eftersom koefficienten framför t²-termen är positiv så vet vi att detta ger minimipunkten (motsvarande parabel ser ut som en smilie face).

Svaret är alltså t = 1/2.

Metod 2 - Hitta stationära punkter med hjälp av derivata

Förstaderivatan av g(t) är g'(t) = 2t-1.

Vi sätter förstaderivatan lika med noll, dvs g'(t) = 0, dvs 2t-1 = 0, dvs t = 1/2.

Vi använder andraderivatan för att ta reda på om detta värde på t är en mi i i- eller maximipunkt:

Andraderivatan g''(t) = 2.

Eftersom g''(1/2) = 2 (vilket är > 0) så är detta en minimipunkt.

Svaret är alltså t = 1/2.

=========

Använd nu någon av dessa metoder på ditt andragradsuttryck g(p) = p²/3-p/2+1/5

Så andra derivatan ger inte mig det största eller det minsta värdet?

Nej, andraderivatans värde vid en stationär punkt ger endast information om den stationära punktens karaktär (minimi- eller maximipunkt).

Läs mitt senaste svar, jag har uppdaterat det.

Läs gärna om andragrafsuttryck, symmetrilinje med mera här.

Samt detta avsnitt som beskriver hur förstaderivatans nollställen kan användas för att hitta stationära punkter.

Samt detta avsnitt som beskriver hur andraderivatan kan användas för att bestämma stationära punkters karaktär (skrolla ner en bit).

Så nu tror jag att jag har allt som du sa

Ja, det är rätt, men eftersom du använde metod 2 så behöver du inte sätta upp ekvationen p²/3-p/2+1/5 = 0.

Vad skulle jag få ha satt för att lösa ut p ?

Arup skrev:

Vad skulle jag få ha satt för att lösa ut p ?

Jag förstår inte riktigt, kan du omformulera frågan?

Yngve skrev:

Arup skrev:

Vad skulle jag få ha satt för att lösa ut p ?

Jag förstår inte riktigt, kan du omformulera frågan?

Eftersom jag använde metod 2 vad hade rätt uppställning varit ?

Du kan skriva som du skrev svar#32, men ta bort raden som börjar med f(p) = 0.