Bestäm för detta värde på b.....
Jag behöver hjälp med följande uppgift men jag vet inte riktigt vad jag ska göra. Det är uppgift b) som jag är osäker på

Jag antar att man löser uppgiften genom: 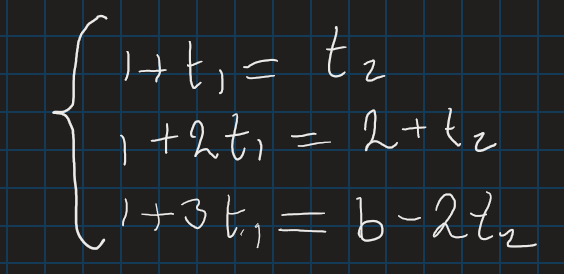
Jag är inte helt säker, men jag ger det ett försök. Vi kan skriva om linjerna så här:
De två vektorerna utan parameter kan tolkas som en ortsvektor som pekar på en punkt på linjerna, och sedan används vektorerna i variabeln för att beskriva alla andra punkter på linjerna. I så fall måste vektorerna och ligga i planet. Dessa är linjärt oberoende och spänner därför upp planet.
Om du kryssar dessa två vektorer så får du en normal till planet. Denna kan du slutligen använda för att entydigt bestämma planets ekvation.
Lösningsförslag
Visa spoiler


Din lösning är tydlig och klart men jag undrar hur du fick (-7, 5, -1) ?
Bazinga skrev:Din lösning är tydlig och klart men jag undrar hur du fick (-7, 5, -1) ?
Det är kryssprodukten av vektorerna.



