Bestäm hastigheten

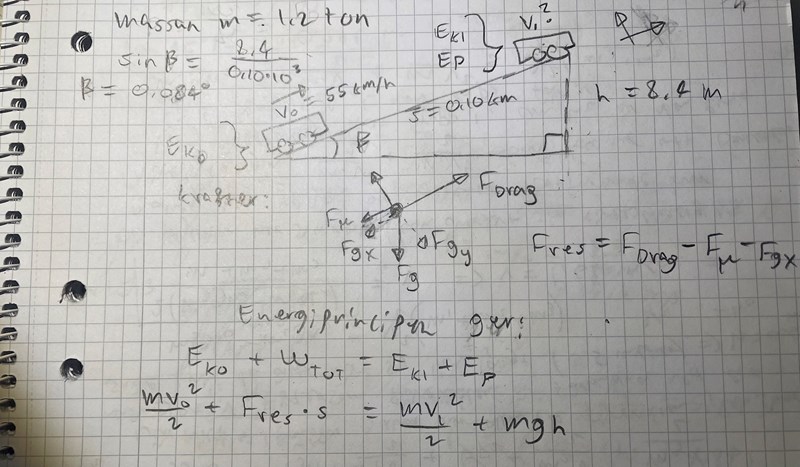
a. Ser min ekvation korrekt ut? När jag satte in värden så fick jag ett imaginärt tal på v1 vilket ju är konstigt
De sista två raderna ser rätt ut.
Visa hur du sedan räknar.
Vi har följande:
Svaret ska bli 12m/s
theg0d321 skrev:Svaret ska bli 12m/s
Det är fel i facit (och ditt svar 4,5 m/s är inte heller rätt).
De har troligtvis glömt att multiplicera kraften Fgx med sträckan 100 meter.
Uttrycket under rotenurtecknet blir negativt, precis som du kom fram till i ditt första inlägg.
Kan du tolka vad det betyder?
Att bilen inte når upp till toppen av backen?
Exakt så. Den stannar alltså en bit upp på vägen.
Extrauppgift: Hur skulle du bära dig åt för att ta reda på hur långt den når?
Eftersom hastigheten v = 0m/s när bilen stannar så vet vi att bilen endast har lägesenergi mgh i den punkt där den står stilla. Då får vi ekvationen
där h är den sökta höjden. Planets lutning samt höjden h kan (med hjälp av lite trigonometri) användas för att beräkna sträckan (hypotenusan) som bilen klarar att åka upp
OK, jag menade att vi vill ta reda på hur lång sträcka längs med backen bilen når.
Den når ju inte 100 meter, men kanske 80? eller 70?
Vi kan ta reda på hur långt den kommer genom att, precis som du skriver, sätta och sedan lösa ut sträckan ur det energisamband som du har satt upp, nämligen .
---------------------------------------------
Ett förenklande tips är att du inte behöver beräkna storleken på vinkeln .
Det enda stället där den förekommer är i , som du ju vet har värdet .


