Bestäm största och minsta värde till funktionen som f(x,y) antar på området
.jpg?width=800&upscale=false)
.jpg?width=800&upscale=false) Hej!
Hej!
Jag hittade inga inre stationära punkter,men jag hade r=1 samt v=pi/2 när jag löste med polära koordinater. Hur ska man fortsätta?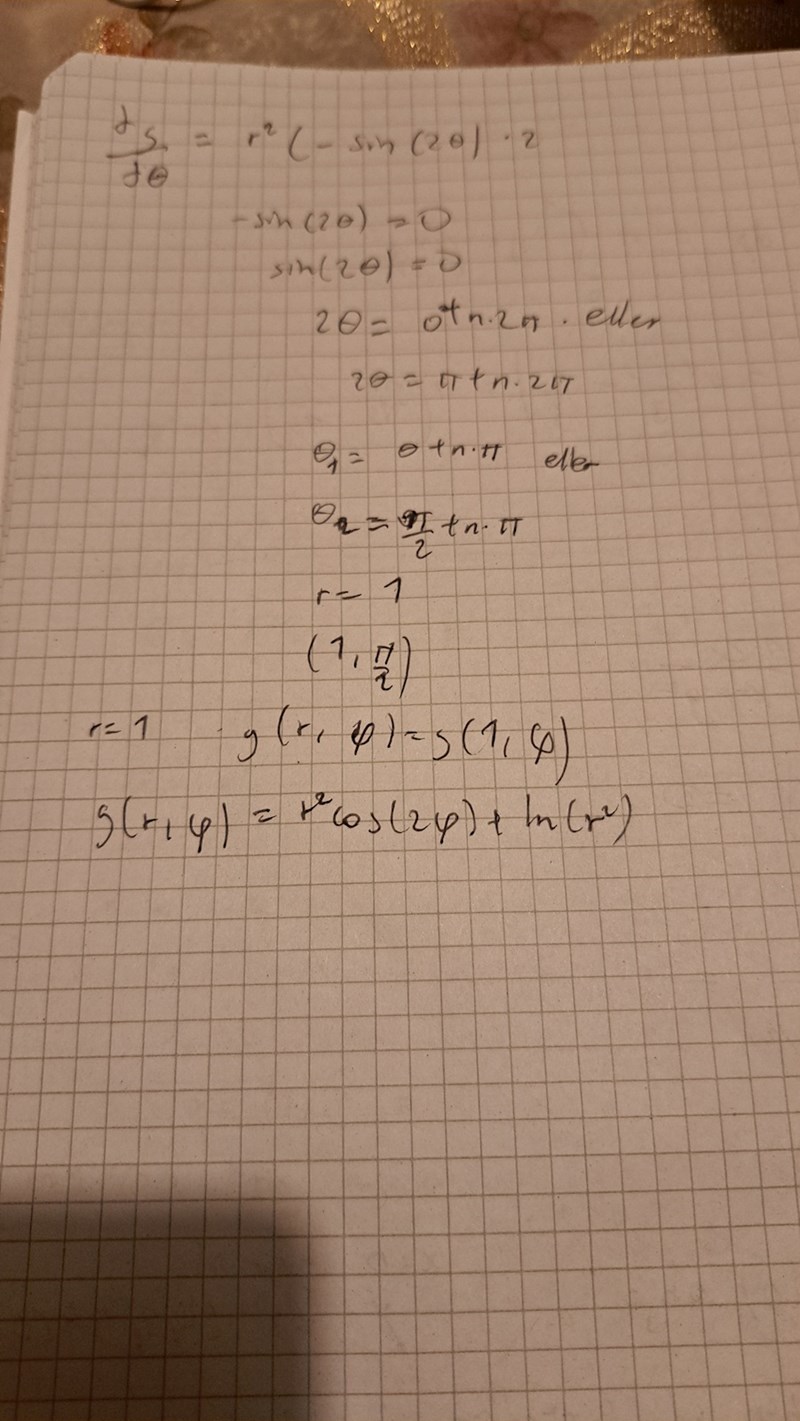
Är det det minsta eller största värdet? Vilket är det andra värdet?
Laguna skrev:Är det det minsta eller största värdet? Vilket är det andra värdet?
Asså jag vet ej om jag behöver undersöka något mer. Fick ju inga inre stationära punkter utan de ligger på randen dvs (0,1) och (0,-1). Men jag hittade en stationär inre punkt (1,pi/2). Ska jag använda den för att hitta max och min? Om jag stoppar in r=1 får jag ju -1 i polära funktionen
Du behöver i alla fall svara på frågan som ställs. Vad är det största och det minsta värdet?
Laguna skrev:Du behöver i alla fall svara på frågan som ställs. Vad är det största och det minsta värdet?
Minsta värdet är -1. Det saknas största värde
r = 1 är den ena randen. Det finns en rand till.
Laguna skrev:r = 1 är den ena randen. Det finns en rand till.
Hm men r=-1 är ej tillåtet ju? Hur hittar jag den andra randen? Jag fick ju förut två lösningar på r där negativa värdet förkastades då r ej får vara negativt som radie.
Rita upp området.
Laguna skrev:Rita upp området.
Menar du att r=2 är andra randen? Hur ska jag hitta fler max och min då nu? Ska man bara stoppa in r=2 i vår parametriserade funktion som innehåller r och sinus/cosinus termer för att se om vi har största eller minsta värde?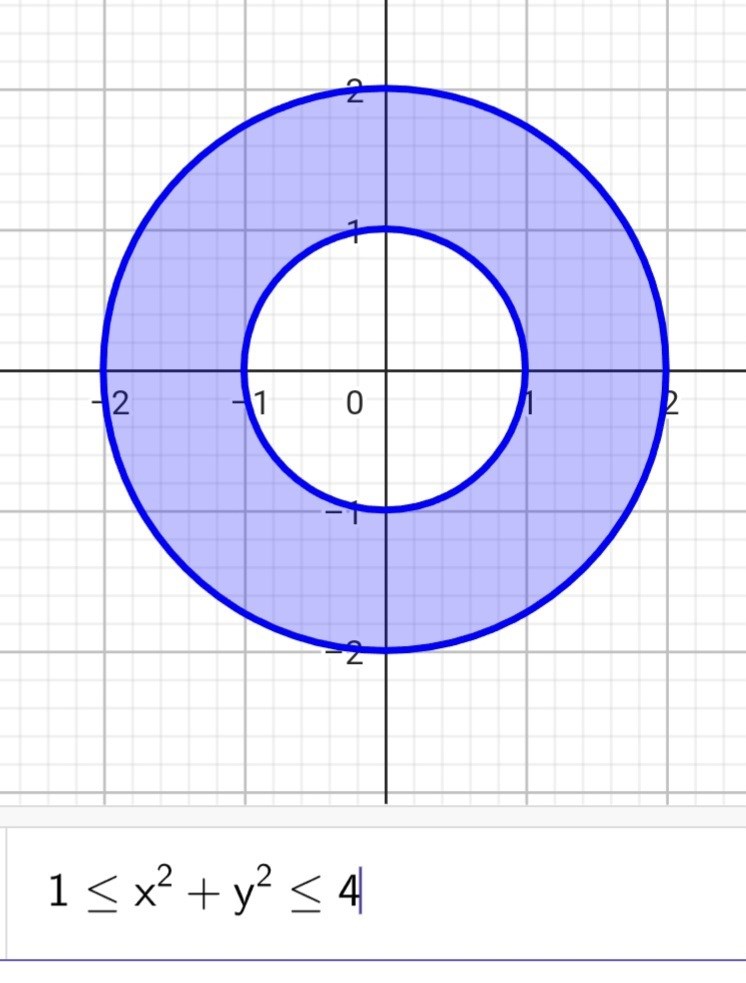
Jag får (1,0) samt (0,1) för ena randen som är stationära punkter. Sen andra randen får jag (2,0) och (0,2). Stämmer de?
Det verkar stämma. Vad är då de största och minsta värdena?
Är inte t.ex. (0, -1) och (-1, 0) också stationära punkter?
Laguna skrev:Det verkar stämma. Vad är då de största och minsta värdena?
Är inte t.ex. (0, -1) och (-1, 0) också stationära punkter?
Hur hittar man (0,-1) och (-1,0) ? Är det bara genom figuren där området är ritad? I mina lösningar så hittade jag ej de negativa värden.
Yta ser ut så här
Det är en bra ide att skriva om till polära koordinater och du får då att
f(r,t) = r^2 cos(2t)+2 ln(r)
Denna funktion är växande m.a.p. r varför den blir mera och mera "extrem" i sin "vågning" desto längre från origo du kommer. "Vågningen" skapas av cos(2t). Därför inträffar max/min på randen där r=2.
Som mest är cos(2t)=1 och som minst -1. För vilka t inträffar det?
Lös ekv. cos(2t)=±1
Trinity2 skrev:Yta ser ut så här
Det är en bra ide att skriva om till polära koordinater och du får då att
f(r,t) = r^2 cos(2t)+2 ln(r)
Denna funktion är växande m.a.p. r varför den blir mera och mera "extrem" i sin "vågning" desto längre från origo du kommer. "Vågningen" skapas av cos(2t). Därför inträffar max/min på randen där r=2.
Som mest är cos(2t)=1 och som minst -1. För vilka t inträffar det?
Lös ekv. cos(2t)=±1
Men varför ska man ej skriva som x=cost, y=sint och sedan x=2cost och y= 2sint?
Då får jag
h(t)=4cos(2t)+ln(4) för r=2 och
för r=1:
g(t)=cost(2t)
Deriverar jag h(t) får jag derivatans nollställena till
t1=0+n*pi
t2=pi/2+n*pi
deriverar jag g(t) får jag derivatans nollställen till
t1=0+n*pi
t2=pi/2+n*pi