Bestäm triangel 2
En variant på den föregående kluringen, men med en extra tvist. Vore intressant att se om även denna går att lösa med olika metoder.
En triangel har vinklarna , och . Motstående sidor är , och , d.v.s. , och .
Det gäller att vinkeln . Sidan längdenheter (l.e.). Vidare är triangelns omkrets
l.e.
Bestäm triangelns vinklar samt de två okända sidorna.
Skriv gärna din lösning inom s.k. spoilers.
Är det tänkt att vinklarna skall vara heltal när de är mätta i grader? Det blir det i alla fall inte när jag försöker, jag får nämligen:
Visa spoiler
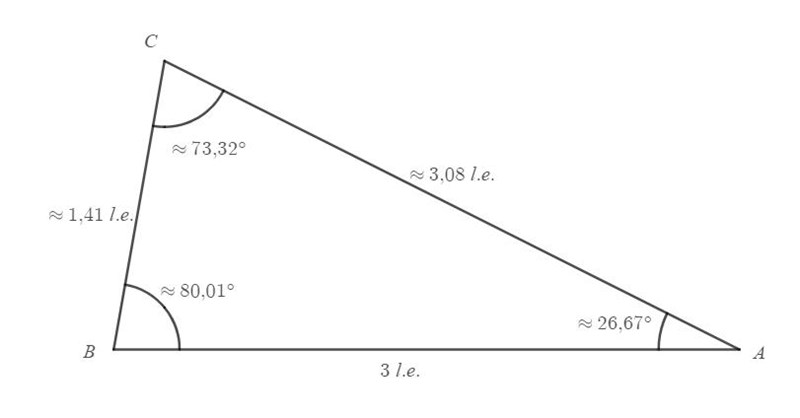
Två av vinklarna ska vara , men hälften av standardvinklar.
Hej AlvinB!
Nu blev det riktigt intressant! Kontrollerade både min och din triangel medelst denna snurra på nätet:
https://www.calculatorsoup.com/calculators/geometry-plane/triangle-law-of-cosines.php
Både ger samma omkrets och att villkoret är uppfyllt. Kan det vara så enkelt att det finns två trianglar som uppfyller de givna villkoren? Det hade jag inte räknat med. I så fall tappas ju en av lösningarna bort i något steg av beräkningen. Går det kanske att se vilket?
Hej igen!
AlvinB, du verkar ha satt istället för , vilket alltså blir en annan triangel. Men rätt räknat utifrån det.
tomast80 skrev:Hej igen!
AlvinB, du verkar ha satt istället för , vilket alltså blir en annan triangel. Men rätt räknat utifrån det.
Nu hänger jag inte riktigt med. I min triangel är väl ?
Jag tror dock jag ser vad som blivit fel. Du har i uppgiften skrivit att sidan har längden , men om det istället skulle stått fås den mycket snyggare lösningen:
Visa spoiler

Kanske var det så det var tänkt?
Ursäkta, jag hade blandat ihop sidorna och . Det var tänkt som du beskrev. Utgick från den triangel du fick fram nu.
Snyggt, AlvinB!



