Bestäm z som uppfyller ekvationen
Hej kan någon se över en sak jag fastnat på?
Uppgift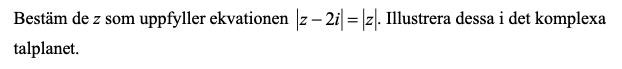
Lösning

Min fråga
Att högerled i det tredje steget blir =fattar jag.
Men att vänsterledet i det tredje steget blir
fattar jag inte?
1) Varför blir z=a i vänsterledet när det i högerledet är z=a+bi
2) Hur härleds (b-2) ?
Jag föredrar en lösning där man endast ritar, medan andra vill lösa uppgiften "algebraiskt".
https://www.pluggakuten.se/trad/bestam-de-z-som-uppfyller-ekvationen/
Om z=a+bi, så är z-2i=a+bi-2i=a+(b-2)i, är du med på det?
Smargdalena:
Det du skriver fattar jag. Men det är ju inte samma som svaret skriver, där finns ju inget i med?: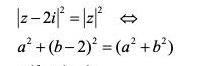
okej men om det ser ut som:
Tänker då att -2 symboliserar tal på reella axeln och därmed konstanten a i z=a+bi.
|z-2i|=|z| skriv om z som z=a+bi
|a+bi-2i|=|a+bi| förenkla VL
|a+(b-2)i|=|a+bi| beräkna absolutbeloppet och kvadrera
a2+(b-2)2=a2+b2 förenkla VL
a2+b2-4b+4=a2+b2 subtrahera a2+b2 från båda leden
-4b+4=0 lös ekvationen
b=1
d v s alla tal som ligger lika långt från origo som från punkten z=2i kan skrivas som den räta linjen z=a+i där a är ett reellet tal.
Tack för ett genomgående svar. Verkligen!
En fråga gällande ditt steg 3 och 4. Blir lite förvirrad där vad som faktiskt händer i övergången?
jag vet ju , men din räkneoperation saknar ju roten ur?
Nej men nu ser jag, du har höjt upp respektive sida med 2 och därmed tagit bort absolubeloppstecknet?
Man får göra vad man vill med en ekvation, bara men gör samma sak på båda sidor. Exempelvis är det tillåtet att kvadrera båda sidor.
Juste!
Ännu en fråga om ni orkar..
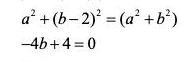
När jag expanderar . Vad händer med med hänseende till nästa steget?
nyfikenpåattveta skrev:Juste!
Ännu en fråga om ni orkar..
När jag expanderar . Vad händer med med hänseende till nästa steget?
Vad menar du med händer?
Eller börja såhär. Vad motsvarar i högerled?
Smaragdalena skrev:|z-2i|=|z| skriv om z som z=a+bi
|a+bi-2i|=|a+bi| förenkla VL
|a+(b-2)i|=|a+bi| beräkna absolutbeloppet och kvadrera
a2+(b-2)2=a2+b2 förenkla VL
a2+b2-4b+4=a2+b2 subtrahera a2+b2 från båda leden
-4b+4=0 lös ekvationen
b=1
d v s alla tal som ligger lika långt från origo som från punkten z=2i kan skrivas som den räta linjen z=a+i där a är ett reellet tal.
Om du har några ikvar när du har räknat ut absolutbeloppen så har du räknat fel. Absolutbeloppet är ett reellt tal och skall inte innehålla något i.
Smaragdalena skrev:|z-2i|=|z| skriv om z som z=a+bi
|a+bi-2i|=|a+bi| förenkla VL
|a+(b-2)i|=|a+bi| beräkna absolutbeloppet och kvadrera
a2+(b-2)2=a2+b2 förenkla VL
a2+b2-4b+4=a2+b2 subtrahera a2+b2 från båda leden
-4b+4=0 lös ekvationen
b=1
d v s alla tal som ligger lika långt från origo som från punkten z=2i kan skrivas som den räta linjen z=a+i där a är ett reellet tal.
Om du har några kvar när du har räknat ut absolutbeloppen så har du räknat fel. Absolutbeloppet är ett reellt tal och skall inte innehålla något .
Smaragdalena skrev:Smaragdalena skrev:|z-2i|=|z| skriv om z som z=a+bi
|a+bi-2i|=|a+bi| förenkla VL
|a+(b-2)i|=|a+bi| beräkna absolutbeloppet och kvadrera
a2+(b-2)2=a2+b2 förenkla VL
a2+b2-4b+4=a2+b2 subtrahera a2+b2 från båda leden
-4b+4=0 lös ekvationen
b=1
d v s alla tal som ligger lika långt från origo som från punkten z=2i kan skrivas som den räta linjen z=a+i där a är ett reellet tal.
Om du har några ikvar när du har räknat ut absolutbeloppen så har du räknat fel. Absolutbeloppet är ett reellt tal och skall inte innehålla något i.
(smiley) Trådskaparen glömde att skriva mellanslag.
"[...]Vad motsvarar i högerled?"
skulle ha skrivits
[..] Vad motsvarar i högerled?
Du har ekvationen -4b+4=0. Lös ekvationen med avseende på b. Du får att b=1, precis som jag redan har skrivit. Alla punkter som ligger lika långt från punkterna z0=0+0i och z2i=0+2i, d v s de värde som satisfierar ekvationen |z-2i|=|z|, ligger på den räta linjen z=a+i.
Som jag tidigare skrivit...jag föredrar att enbart rita.
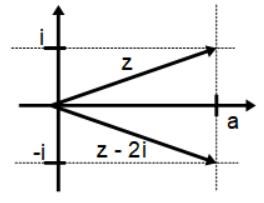
Jag förstår inte Affes bild. Så här skulle jag göra:
- Rita ett komplext talplan.
- Markera de båda taoen 0+0i och 0+2i.
- Markera den punkt som ligger mitt emellan de båda komplexa talen, d v s 0+i
- Rita en linje genom denna punkt som är vinkelrät mot linjen genom 0,0i och 0+2i. Du har ritat linjen Im(z)=1.
Smaragdalena skrev:Jag förstår inte Affes bild. Så här skulle jag göra:
- Rita ett komplext talplan.
- Markera de båda taoen 0+0i och 0+2i.
- Markera den punkt som ligger mitt emellan de båda komplexa talen, d v s 0+i
- Rita en linje genom denna punkt som är vinkelrät mot linjen genom 0,0i och 0+2i. Du har ritat linjen Im(z)=1.
Ser du att längderna (beloppen) av de två pilarna (vektorerna) är lika?
Behåll avståndet "2i" och förflytta pilspetsarna utmed den vertikala punktade linjen "a". Hur går det då med längderna (beloppen) av de två pilarna (vektorerna)?
Tackar för er hjälp har fått tillräcklig input för denna fråga nu :)
Affe Jkpg skrev:Smaragdalena skrev:Jag förstår inte Affes bild. Så här skulle jag göra:
- Rita ett komplext talplan.
- Markera de båda taoen 0+0i och 0+2i.
- Markera den punkt som ligger mitt emellan de båda komplexa talen, d v s 0+i
- Rita en linje genom denna punkt som är vinkelrät mot linjen genom 0,0i och 0+2i. Du har ritat linjen Im(z)=1.
Ser du att längderna (beloppen) av de två pilarna (vektorerna) är lika?
Behåll avståndet "2i" och förflytta pilspetsarna utmed den vertikala punktade linjen "a". Hur går det då med längderna (beloppen) av de två pilarna (vektorerna)?
Din tjocka linje har Im(z)=0, inte Im(z)=1 som den borde. Eller tolkar jag din bild helt fel?
Det komplexa planet har en axel för imaginära delen och en axel för reella delen av ett komplext tal.
Min tjocka linje...kan Smaragdalena mena axeln för den reella delen av ett komplext tal?
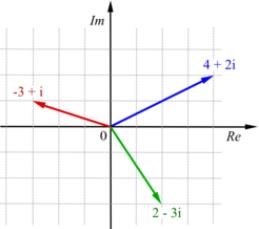
Nedan har du tre exempel på komplexa tal.
Tydligen förstår jag inte din bild alls, Affe. Så här ser min bild ut:
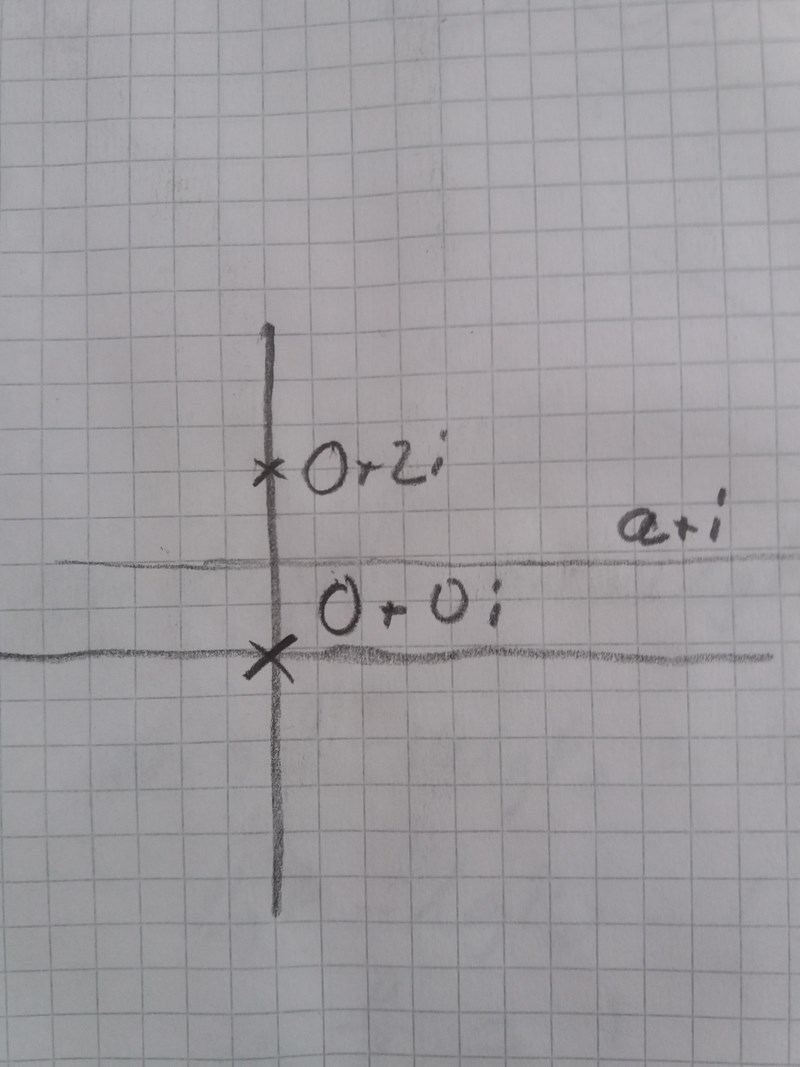
Smaragdalena skrev:Tydligen förstår jag inte din bild alls, Affe. Så här ser min bild ut:
Röd pil är lika med z och z = a + i där a och Im(z) = 1
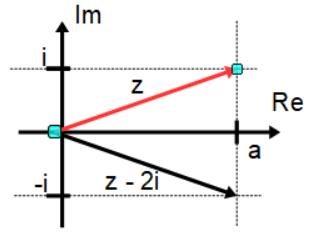
Jag tror jag förstår hur du tänker, men för mig är det en förfärlig omväg. Intressant att man kan täkna så olika!
Förstår nu! Tack för input och att få skriva av sig :)





