Bestämma dimension till värderum och bas för nollrum till linjär avbildning på \mathcal{P}_3
Halloj!
Jag sitter med uppgiften nedan:
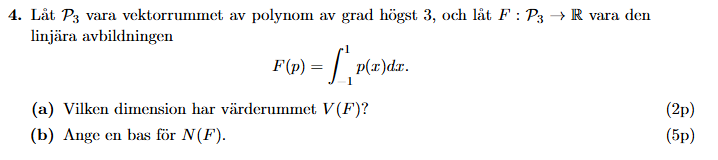
Angående (a) tänker jag helt enkelt att , eftersom kodomänen till är och alla reella tal kan uttryckas som , där är basvektorn och är en reell skalär.
Angående (b) tänkte jag att man kan börja med att konstatera att enligt dimensionssatsen. Sedan kan vi ansätta och beräkna:
Om vi sedan sätter detta lika med noll får vi att polynomen i basen måste uppfylla det linjära villkoret . Vi kan alltså variera paramterarna och hur vi vill så länge de tre polynomen förblir linjärt oberoende. Således skulle vi kunna föreslå basen:
Är detta rätt tänkt?
Är dina bas-polynom linjärt oberoende?
Jag ser nu att jag råkade skriva fel, jag menade:
Men du har helt rätt. Det finns en linjärkombination av det andra och det tredje polynoment som ger . Därför föreslår jag istället:
Detta borde väl vara en giltig bas?
Jo, men räcker det inte om den sista vektorn bara är x?
Jo, det hade väl räckt egentligen...!
Jag hade bara snöat in mig på sambandet mellan och , fastnat i ett tankespår, så att säga...
Men du har givetvis rätt.
Är resonemangen rätt i övrigt?
Ja, det ser rätt ut.
Du skulle kanske kunna förtydliga ditt argument för varför V(F) har dimensionen 1. Det låter som att du (helt korrekt) säger att dim(R)=1, men det saknas en rad om varför V(F)=R.
Jag ville inte uttala mig om huruvida , för jag visste inte om det stämde. Däremot tänkte jag att och är ett vektorrum över med dimension 1. I så fall måste .
(Hoppas jag använde terminologin rätt)
Här är ett enkelt men viktigt faktum om underrum som du kan försöka bevisa som en extra övningsuppgift (säg till om du kör fast!).
Lemma. Om U är ett underrum till ett vektorrum V, så gäller följande:
- dim(U) <= dim(V);
- dim(U) = dim(V) <=> U = V.
Av detta följer att det bara finns två möjligheter:
- dim(V(F))=1 [vilket är ekvivalent med V(F)=R]
- dim(V(F))=0 [vilket är ekvivalent med V(F)={0}].
Det räcker alltså att visa att V(F) innehåller minst en nollskild vektor för att sluta sig till att dim(V(F))=1 (och att V(F)=R).
Jag vet inte riktigt hur man ska visa detta formellt, men det känns ju som en extremt rimlig sats. Man kan kanske börja så här:
Låt vara ett vektorrum med bas . Då kan varje element skrivas:
Låt vidare vara ett underrum till med bas . Eftersom alla också ligger i , kommer alla sådana kunna skrivas:
I fallet då är . Om vi inte ska ha att måste vara en mängd på formen:
Men om en eller flera koefficienter ständigt är noll innebär det att de ihophörande basvektorerna inte ingår i , och då måste .
oggih skrev:Lemma. Om U är ett underrum till ett vektorrum V, så gäller följande:
- dim(U) <= dim(V);
- dim(U) = dim(V) <=> U = V.
Bara en liten kommentar till lemmat:
Andra punkten om likheten av dimensionerna/rummen gäller endast om vektorrummet V har en ändlig dimension.
I oändlig-dimensionella rum kan det nämligen hända att dim(U)=dim(V)=, men .
(I denna diskussionstråd har alla relevanta vektorrum en ändlig dimension, så det är inga problem här)
LuMa07 skrev:
Bara en liten kommentar till lemmat:
Andra punkten om likheten av dimensionerna/rummen gäller endast om vektorrummet V har en ändlig dimension.
I oändlig-dimensionella rum kan det nämligen hända att dim(U)=dim(V)=, men .
Bra och viktig poäng!
Är resonemanget jag föreslog i #10 korrekt, förutsatt att vi arbetar med ändligtdimensionella vektorrum?
naytte skrev:Är resonemanget jag föreslog i #10 korrekt, förutsatt att vi arbetar med ändligtdimensionella vektorrum?
Nja, inte riktigt.
Om du tänker dig med standardbasen och ett snett plan med basen , så gäller det inte att . U:s basvektorer är just sådana att för alla .
Visa spoiler
Antag att resp. är baser för och , där . Då är och .
Om , så gäller olikheten per automatik och det finns inget att bevisa.
Antag att . Låt . Varje av basvektorerna kan skrivas som en unik linjärkombination av vektorerna , d.v.s. för varje . Det finns alltså en uppsättning av koefficienter som anger samband mellan baserna.
Om , så kan man via gausselimination (där är koefficientmatrisen) hitta en linjärkombination av sådant att denna linjärkombination är lika med nollvektorn, vilket skulle motsäga linjärt oberoende av . Därmed måste .
(Det kanske finns något enklare bevis...)




