Bestämma extrempunkter för flervariabel funktion på cirkelskiva

Precis, $\nabla f = 0$ ger dig extrempunkter inom området.

För randen kan man använda Lagrange metod. Den går ut på att man definierar bivillkoret som en funktion $g(x,y)$ och tittar på var gradienten av $f$ och $g$ är parallella. Där finns det en extrempunkt.

Tack för tipset! Ska kolla in Lagranges metod.

Men för att vara tydlig angående kriteriet $\nabla f = 0$; då vi plockar fram extrempunkter enligt detta kriterium måste vi bekräfta att de faktiskt ligger inom cirkeln, eller hur? Och sedan kan man använda Lagranges metod, som jag ska läsa på om nu, just för randen?

Det vanligaste sättet att lösa dessa problem på är genom, som nämnt, Lagranges metod. Emellertid, vissa optimeringsproblem kan lösas med hjälp av algebra:

naytte skrev:

Tack för tipset! Ska kolla in Lagranges metod.

Men för att vara tydlig angående kriteriet $\nabla f = 0$; då vi plockar fram extrempunkter enligt detta kriterium måste vi bekräfta att de faktiskt ligger inom cirkeln, eller hur? 

Och sedan kan man använda Lagranges metod, som jag ska läsa på om nu, just för randen?

Ja precis, på båda frågor. Funktionen har ju egentligen inget med vår avgränsning att göra. 

Om man inte vill använda sig av Lagrangemultiplikatorer för att hitta eventuella extrempunkter på randen, så kan man också parametrisera cirkeln med (förskjutna) polära koordinater:

$\left\{\begin{array}{rl}x(t)&=-1 + \cos t\\y(t)&=1 + \sin t\end{array}\right.$

där parametern $t$ går ett varv, t.ex. $t \in [-\pi, \pi]$. För punkten $(x,y)$ på randen gäller alltså att:

$\begin{array}{rl}f(x,y)&=f(-1+\cos t,1+\sin t)\\&=(-1+\cos t)(1+\sin t)-(-1+\cos t)+(1+\sin t)\\&=1+\cos t\sin t=1+\frac{\sin2t}{2} \end{array}$

vars extremvärden är $1\pm1/2$, vilket antas i punkterna där $t = \pm\pi/4$ eller $t=\mp 3\pi/4$.

(Vad som händer innanför cirkelskivan får undersökas via stationära punkter, d.v.s. genom att lösa ekvationen $\nabla f(x,y) = 0$)

Tack för förslaget! Det var det jag tänkte göra! :D

En fråga om $\nabla f(x,y)=0$:

Om man ställer upp ekvationen så får man får ett ekvationssystem som "redan är löst". Om jag har tänkt rätt får jag systemet:

$\displaystyle \left\{\begin{array}{rl}\frac{\partial f}{\partial x}&=y-1=0\\ \frac{\partial f}{\partial y}&=x+1 =0\end{array}\right.$

Vi har alltså att det ska finnas ett extremum i $(-1,1)$. Men varför får vi bara en lösning här? Då vi kollar specifikt på randen får vi ju många fler lösningar. Borde inte dessa dyka upp här också? 

EDIT: ser nu att frågan bad om största och minsta värde, inte bara extrempunkter. Det förklarar saken. På en "sluten definitionsmängd" i $xy$-planet kan funktionsytan såklart t.ex. anta ett största värde utan att det är en extrempunkt för funktionen.

Bara för att bekräfta att jag har kommit fram till rätt svar, får ni också att största värdet blir $3/2$ och att minsta är $1/2$? Tydligen så spelade den stationära punkten ingen roll, utan både det största och minsta värdet låg på randen.

naytte skrev:

Bara för att bekräfta att jag har kommit fram till rätt svar, får ni också att största värdet blir $3/2$ och att minsta är $1/2$? Tydligen så spelade den stationära punkten ingen roll, utan både det största och minsta värdet låg på randen.

Mathematica ger min/max:

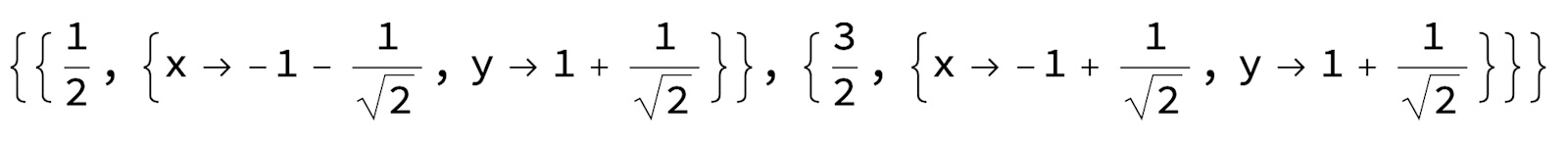
Grafen påminner om "Pringles";

Jag begriper inte riktigt vad jag tittar på. Är det min = 1/2 och max = 3/2 med de värden på $x$ och $y$ som ger dessa värden?

Och jag tänkte också på att det såg ut som ett pringleschips! :D

naytte skrev:

Jag begriper inte riktigt vad jag tittar på. Är det min = 1/2 och max = 3/2 med de värden på $x$ och $y$ som ger dessa värden?

Och jag tänkte också på att det såg ut som ett pringleschips! :D

Ja, utformatet är först funktionsvärdet och sedan följer x/y-koordinaten

Okej, nice! Då blev det rätt! :D

Tack för hjälpen till alla i tråden!