Bestämma konstant c för luftmotstånd "som i boken" för matematisk pendel

Halloj!

Jag håller på att skriva en laborationsrapport på en labb om en matematisk pendel. Vi hade ett kamerasystem som höll reda på pendelns position inom ett av mjukvaran definierat koordinatsystem $xyz$. 

Enligt instruktioner har jag precis anpassat en funktion:

$\displaystyle \theta(t)=\theta_0e^{-\zeta\omega t}\sin(\omega t+\delta)$

till utslagsvinkeln vid varje mätpunkt i en mätning. Nu står det däremot att jag ska göra följande:

I kapitel 6.4b i boken har de däremot en harmonisk oscillator som modellsystem. Detta rör sig naturligtvis endast i en dimension med hastighet $v=\dot x$. De inför en fjäderkraft $-kx$ samt en dämpande kraft $-c\dot x$, och definierar sedan:

$\displaystyle\zeta = \frac{c}{2\sqrt{km}}$

Vårt system är ju dock en pendel och har alltså dels flera dimensioner för rörelse och dels ingen fjäderkonstant. Jag förstår inte hur jag ska räkna om vår dämpningskonstant $\zeta$ på samma sätt som i boken. Jag antar att man kan försöka "översätta" vårt system till en harmonisk oscillator på något sätt men jag förstår inte hur.

Jag har gjort en liten skiss nedan:

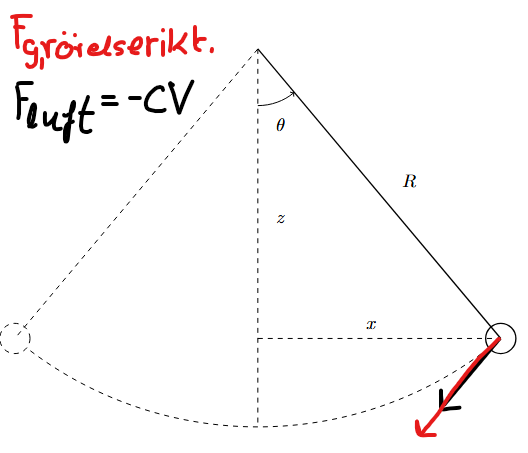
Jag tänker att man borde kunna tillämpa Newton II här och säga att:

$\displaystyle -mg\sin\theta- c\sqrt{\dot{x}^2 + \dot{z}^2} = m\sqrt{{\ddot{x}}^2 + {\ddot{z}}^2}$

Men detta är nog inte vad de frågar efter.