Bestämma konvergensradie för potensserie som satisfierar diff. ekvation
Halloj!
Jag sitter med och sliter snart av mig höret över uppgiften nedan:
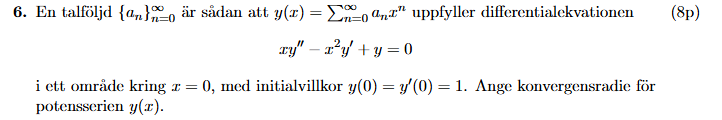
Jag började med att ta fram uttryck för samt :
Sedan stoppar jag in dessa i differentialekvationen, för att försöka dra några slutsatser om :
Sedan försökte jag för varje summa göra ett passande indexskifte för att tillrättalägga exponenterna för och kom då fram till:
För den första termen är de två första deltermerna noll, så vi kan börja indexeringen från . För den tredje termen kan vi plocka ut den första delsumman som bara ger och vi erhåller:
Vi kan skriva ihop allt som en summa:
Vidare vet vi att ur initialvillkoret , så ekvationen kan slutligen skrivas som:
Detta känns dock helt fel. Hur kan vi få ett polynom av grad i HL?? Någonting har gått fel men jag förstår inte var. Är inte detta en motsägelse?
Det måste vara fel i uppgiften.
Om man sätter in i själva differentialekvationen , så får man .
Begynnelsevillkoret motsäger den givna differentialekvationen.
Jag tjuvkikade efter en del irritation i facit:
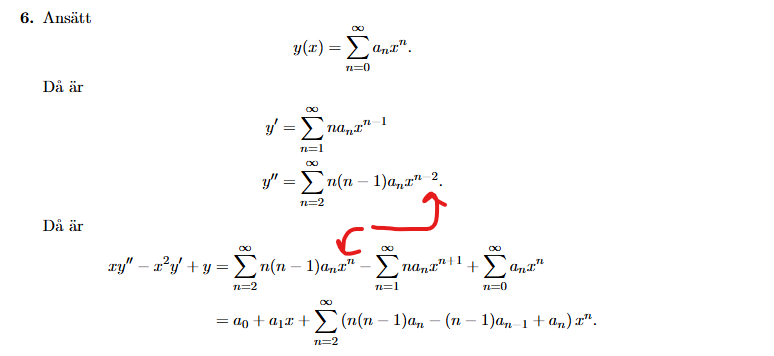
Tentamakaren hade råkat få n-1 till n och kanske därför inte upptäckt felet själv?
naytte skrev:Tentamakaren hade råkat få n-1 till n och kanske därför inte upptäckt felet själv?
Visst det där är ett fel, men även med denna felaktiga exponent får man en motsägelse i differentialekvationen då enligt begynnelsevillkoret, men hela uttrycket på sista raden i skärmbilden skall vara lika med noll, vilket ej är möjligt p.g.a. entydigheten av potensserieutvecklingar.
Okej, tack!
Ska maila honom och påpeka att det har blivit lite fel i hans frågeställning. Det är ju bra för framtida studenter att slippa förvirras som jag.
Men en fråga till: hade mitt tillvägagångssätt fungerat förutsatt att initialvillkoren hade angetts rätt? dvs. låt säga att vi fick . Hade min metod med omskrivning med indexskifte osv. fungerat?
naytte skrev:... Hade min metod med omskrivning med indexskifte osv. fungerat?
Har snabbt kollat igenom uträkningen och den verkar ok.
Det är dock en sak som jag inte är förtjust av, nämligen att serierna för och startar med och därmed innehåller termer med respektive . Koefficienterna vid dessa termer är visserligen lika med 0, så det gör inget egentligen, men det känns märkligt att en konstant term får som sin derivata.
(När du kollar i facit, så startar serien för med och för med .)
Nu har du fått fram det rekursiva sambandet för alla med begynnelsevillkoren och . Det återstår att bestämma konvergensradien, exempelvis med d'Alemberts kvotkriterium. (Notera att man inte behöver ta fram någon explicit formel för .)
Hur ska man tillämpa kvotkriteriet här utan att explicit känna ? Vi vill alltså använda kriteriet:
Kan vi alltså helt enkelt stoppa in , dela båda led med och låta i båda led? Alltså:
?
Lös ut ur det rekursiva sambandet och dividera båda leden med :
.
Om man definierar , så säger ekvationen ovan att .
I kvotkriteriet vill man hitta gränsvärdet .
Om man skickar i ekvationen , så får man , där . (Man behöver dock motivera att detta gränsvärde faktiskt existerar.)


