Bestämma punkt i triangel med vektorprodukt
Hej!
I uppgiften: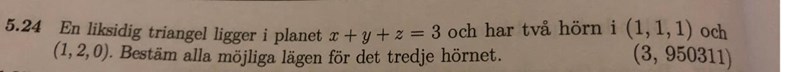
Har jag fastnat. Jag tänkte att man kunde använda sig av normalen till planet (1, 1, 1) och vektorn
för att göra vektorprodukten
Men då får jag att
Vilket inte verkar stämma, någon som kan ge ett tips på hur jag kan göra istället?
Punkten (a,b,c) ligger lika långt ifrån (1,1,1) som (1,2,0) och koordinaterna uppfyller
a + b + c = 3
Kryssprodukten (0, 1, -1) x (1, 1, 1) kanske kan vara något.
Brute Force
Du får två vektorer som beskriver sökt punkt relativt punkterna och :
Vi vet längden på vektorerna genom att vi vet att:
Därmed får vi att:
Detta ger:
Eftersom vi har får vi att:
Nu kan du lösa för "möjliga lägen" hos det tredje hörnet.
Elegant
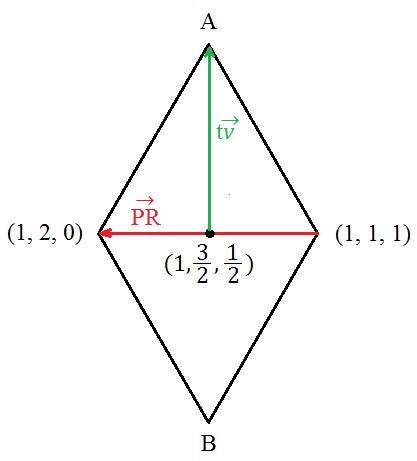
Riktningsvektorn som pekar till möjliga lägen är:
Längden på en vektor som pekar till möjliga lägen är:
Där . Vi får därför genom faktumet att det är en liksidig triangel att:
Således får vi våra möjliga lägen som:
Om du inte hängde med på ovan så har du här en bild som illustrerar lite: