Bevisa att F(v_i) är en bas för V om N(F) = {0_V}

Halloj!

Jag sitter med a)-uppgiften nedan:

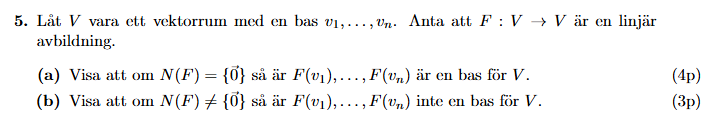
Mitt försök framgår nedan, och jag undrar om jag har tänkt rätt.

Låt $x\in V$. Det följer att $x$, för passande koefficienter $\alpha_1,\alpha_2,...,\alpha_n$, kan skrivas:

$\displaystyle x=\sum_{i=1}^{n}\alpha_iv_i$

Detta innebär alltså att:

$\displaystyle F\left(x\right)=F\left(\sum_{i=1}^{n}\alpha_iv_i\right)=\sum_{i=1}^{n}\alpha_iF\left(v_i\right)$

Detta innebär att värderummet $V(F)$ spänns upp av $F(v_1),F(v_2),...,F(v_n)$.

Enligt dimensionssatsen har vi att $\dim N(F) + \dim V(F) = \dim V$. Eftersom $N(F) = \{0_V\}$ följer det att $\dim V(F) = \dim V$, och eftersom $V(F)$ är ett underrum till $V$ följer det dessutom att $V(F) = V$. Detta medför att $F(v_1),F(v_2),...,F(v_n)$ även spänner upp $V$.

Eftersom det enda elementet som $F$ avbildar på nollvektorn är nollvektorn vet vi att ekvationen $\sum_{i=1}^{n}\alpha_iF(v_i)=F\left(\sum_{i=1}^{n}\alpha_iv_i\right)=0_V$ uppfylls endast då:

$\displaystyle \sum_{i=1}^{n}\alpha_iv_i=0_V$

och denna ekvation satisfieras endast av $\alpha_1,\alpha_2,...,\alpha_n = 0$, ty $v_1,v_2,...,v_n$ är linjärt oberoende från defintionen av $V$.

Eftersom $F(v_1),F(v_2),...,F(v_n)$ spänner upp $V$ och är linjärt oberoende utgör $F(v_1),F(v_2),...,F(v_n)$ en bas till $V$.

$\blacksquare$