Bevisa delbarhet med 3
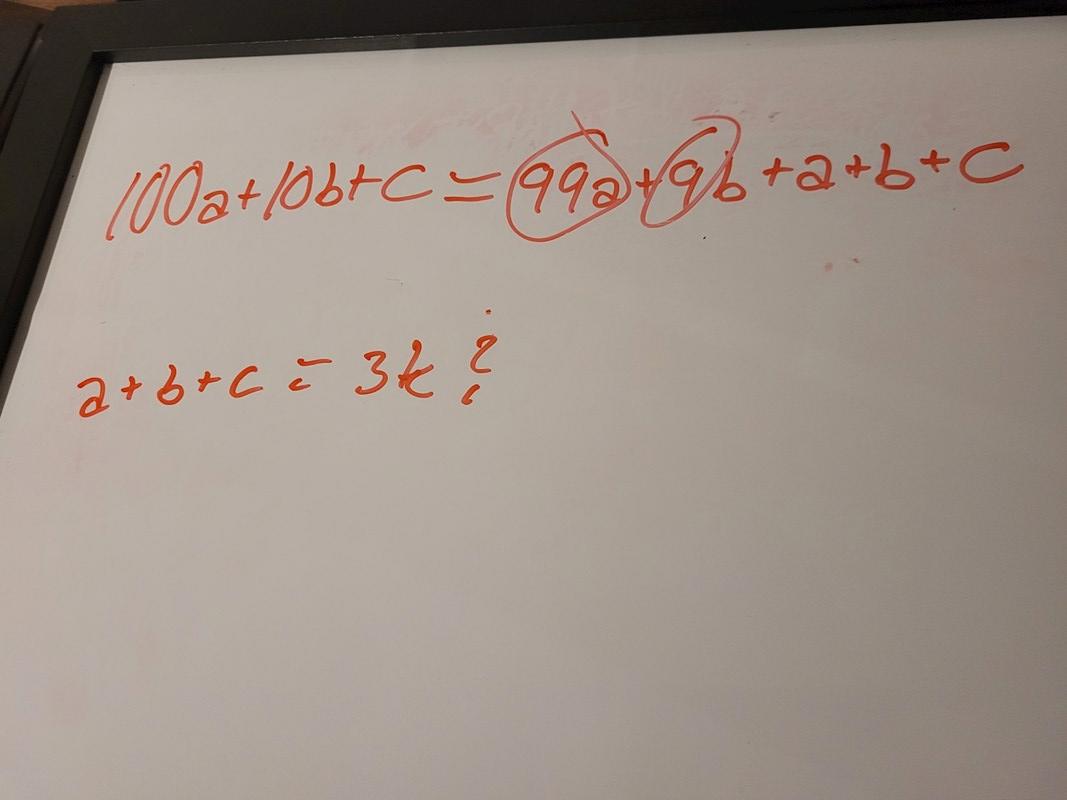1064. a) Visa generellt att om ett tresiffrigt tal är delbart med 3 så är dess siffersumma delbart med 3.
Hur ska man kunna visa detta?
Jag har skrivit upp och skrivit om
100a + 10b +c = 99a + 9b + a + b + c
Jag fattar att 99a och 9b är delbart med tre för att man kan bryta ner dessa i primfaktorer som innehåller 3 men jag ser ingen väg att bryta ner a+ b + c!
Hur visar jag att siffersumman är delbart med 3?
a + b + c = 3k?
Bra start!
Om vi antar att 100a+10b+c är delbart med 3 krävs det att a+b+c också är delbart med 3. Det inses så som du skriver
Eftersom talet 100a+10b+c är dekbart med 3 så måste 99a+9b+a+b+c vara delbart med 3.
99a+9b = 9•(11a+b) = 3•3•(11a+b) är delbart med 3. Alltså måste även a+b+c vara delbart med 3.
Jag ser det fortfarande inte. 100 och 10 står med bara för att illustrera position. Det tresiffriga talet abc är alltså skrivet i utvecklad form. Lösningsförslaget i boken säger
"Antag att talet är delbart med tre"
Ja men då borde jag ju bara kunna skriva
a+b+c = 3k?
Variablerna (a, b, c) kan bara vara ett tal mellan 1 och 9, eller 0?
Jag får sova på saken så kanske det lossnar.
100a + 10b + c = 3n
a + b + c = 3n - 99a - 9b = 3n - 3(33a + 3b) = 3n - 3m = 3 (n-m) = 3k
n,m,k är alla heltal
Och du kan använda samma logik med 999, 9999 osv.
StudieRo skrev:Jag ser det fortfarande inte. 100 och 10 står med bara för att illustrera position. Det tresiffriga talet abc är alltså skrivet i utvecklad form. Lösningsförslaget i boken säger
"Antag att talet är delbart med tre"
Ja men då borde jag ju bara kunna skriva
a+b+c = 3k?
Variablerna (a, b, c) kan bara vara ett tal mellan 1 och 9, eller 0?
Jag får sova på saken så kanske det lossnar.
Nej, man menar verkligen att det ursprungliga talet ÄR 100a+1+b+c. Detta kan skrivas om till (99+1)a+(9+1)b+c, som i sin tur kan skrivas om till 99a+9b+a+b+c. Att 99a och 9b hoppar jag är självklart. Eftersom vi antog från början att talet är delbart med 3, så måste a+b+c (d v s siffersumman) vata delbart med 3, annars kunde inte hela talet vara delbart med 3.
Visst, variablerna a b och c kan vara siffrorna mellan 0 och 9, men om talet-från-början är delbart med 3, så kan det inte vara vilken kombination av dessa siffror som helst.
Hoppas du har sovit gott!
