Cirklar i liksidig triangel
Hej!
Här kommer en liten geometrikluring.
I en liksidig triangel med sidan ritas cirkelsektorer med samma radie från två av hörnen. Cirkelsektorerna och triangeln begränsar ett område inuti triangeln. Sträckan där området angränsar mot triangeln har längden . Bestäm områdets area.

Jag tänker så här...
Säg att nedre vänstra hörnet är origo. Cirklarna skär varandra i x=2,5 vilket innebär att det skuggade området slutar vid x=3. Området är alltså dubbelt så stort som integralen av den funktion som beskriver den vänstra cirkelsektorn (med radie 3), beräknad från x=2,5 till x=3:
Jag erkänner att jag inte orkar lösa den där integralen "för hand" utan använde räknare, men området torde alltså vara ca 1,13 areaenheter, vilket verkar rimligt.
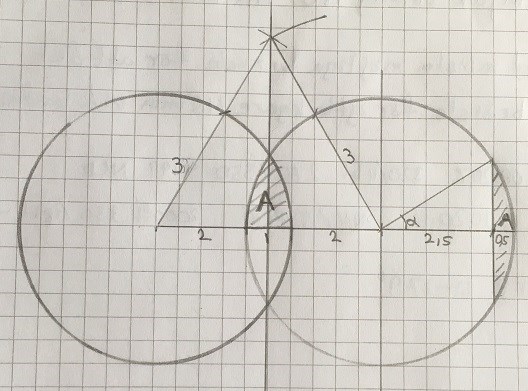
Om vi ritar ut cirklarna så ser vi att arean är densamma som cirkelsektorn längst till höger i bilden.
Vi kan räkna ut vinkeln alfa då vi känner till x och
Med hjälp av trigonometriska ettan kan vi få fram att
Cirkelsegmentets raka del och bågen
Sedan kan vi använda
Jag får det till A = 1,42 a.e. men det känns inte som en elegant lösning med ett exakt svar.
Borde gå att få till bättre?
Edit: Kan det vara så att svaret är ?
Skulle också kunna beräkna cirkelsektorns area och dra bort triangeln för att få den där yttre remsan kvar. Då får jag samma som Russell.
Vad är det för areaformel du använt, Conny?
Skaft skrev:Skulle också kunna beräkna cirkelsektorns area och dra bort triangeln för att få den där yttre remsan kvar. Då får jag samma som Russell.
Vad är det för areaformel du använt, Conny?
Det är ur Karlebo handbok, men finns också på nätet bl.a. denna länk
och ser ut så här: Ja det låter som en lite enklare variant än min. Får du samma svar som Russel?
Ja det låter som en lite enklare variant än min. Får du samma svar som Russel?
Russel & Skaft har fått rätt svar! Snyggt! Är det någon av er som vågar er på att ta fram ett exakt svar?
Connys areaformel ser ut att fungera - men du glömmer att bågen också skall multipliceras med (radien)! När du räknar stoppar du ju bara in vinkeln, men du borde stoppa in båglängden.
AlvinB skrev:Russel & Skaft har fått rätt svar! Snyggt! Är det någon av er som vågar er på att ta fram ett exakt svar?
Connys areaformel ser ut att fungera - men du glömmer att bågen också skall multipliceras med (radien)! När du räknar stoppar du ju bara in vinkeln, men du borde stoppa in båglängden.
Nej jag har med radien i min beräkning. Det var bara ett slarvfel när jag skrev formeln att jag glömde skriva ut r för radien, men
jag får fortsätta senare. Just nu har vi ett barn-barn hemma :-)
Det jag knappade in på wolfram var
Räknas det som ett exakt svar, eller kan man få nåt utan arccos?
ConnyN skrev:AlvinB skrev:Russel & Skaft har fått rätt svar! Snyggt! Är det någon av er som vågar er på att ta fram ett exakt svar?
Connys areaformel ser ut att fungera - men du glömmer att bågen också skall multipliceras med (radien)! När du räknar stoppar du ju bara in vinkeln, men du borde stoppa in båglängden.
Nej jag har med radien i min beräkning. Det var bara ett slarvfel när jag skrev formeln att jag glömde skriva ut r för radien, men
jag får fortsätta senare. Just nu har vi ett barn-barn hemma :-)
Ja, då kanske det är så enkelt som ett miniräknarfel.
Jag får nämligen rätt svar (samma som Russell) när jag använder din formel.
Skaft skrev:Det jag knappade in på wolfram var
Räknas det som ett exakt svar, eller kan man få nåt utan arccos?
Helt rätt!
Den där vinkeln () visar sig vara omöjlig att uttrycka som en rationell multipel av , så vi får nog nöja oss med det där uttrycket.
AlvinB skrev:ConnyN skrev:AlvinB skrev:Russel & Skaft har fått rätt svar! Snyggt! Är det någon av er som vågar er på att ta fram ett exakt svar?
Connys areaformel ser ut att fungera - men du glömmer att bågen också skall multipliceras med (radien)! När du räknar stoppar du ju bara in vinkeln, men du borde stoppa in båglängden.
Nej jag har med radien i min beräkning. Det var bara ett slarvfel när jag skrev formeln att jag glömde skriva ut r för radien, men
jag får fortsätta senare. Just nu har vi ett barn-barn hemma :-)Ja, då kanske det är så enkelt som ett miniräknarfel.
Jag får nämligen rätt svar (samma som Russell) när jag använder din formel.
Nej jag hade slarvat i uppställningen också. Det som var lustigt var att när jag satte in alla uppgifter i formeln och förkortade så kom jag nästan till samma formel som Skaft med "min" formel.
känner jag inte till. Vi hade ett avsnitt i arcusfunktioner på gymnasiet 1971, men jag kommer inte ihåg det riktigt.
Jag hittar inget i mina nya gymnasieböcker från Origo, matte 4 och matte 5.
Går det att förklara lite kort för mig? Så jag kan ersätta med
Lägg inte ner för mycket arbete på förklaringen om det är svårt. Jag kommer väl förr eller senare dit också så småningom.
arccos är samma funktion som , så skillnaden mellan våra uttryck är bara att jag har 9 där du har . Hur jag hamnar där:
Cirkelsektorns area = ,
dvs. cirkelns area gånger den andel som vinkeln täcker av ett helt varv (med radianer som vinkelenhet). Förenklat:
där radien är 3 och vinkeln är : .
Skaft skrev:arccos är samma funktion som , så skillnaden mellan våra uttryck är bara att jag har 9 där du har . Hur jag hamnar där:
Cirkelsektorns area = ,
dvs. cirkelns area gånger den andel som vinkeln täcker av ett helt varv (med radianer som vinkelenhet). Förenklat:
där radien är 3 och vinkeln är : .
Aha jag mindes inte helt fel då jag trodde att cos-1 eventuellt var samma sak som arccos.
Tack för förklaringen den passar bra till kapitlet jag repeterar i matte 4 med radianer och trigonometri.
Det är inte helt lätt att förstå vad man ska ha radianer till, men det kommer en och annan godbit i taget :-)
Tack AlvinB, Russel och till dig Skaft. Hoppas ni får en trevlig lördagskväll!
Det är inte helt lätt att förstå vad man ska ha radianer till, men det kommer en och annan godbit i taget :-)
När du skall derivera eller integrera trigonometriska funktioner så är det väldigt mycket enklare om man arbetar med radianer.
Smaragdalena skrev:Det är inte helt lätt att förstå vad man ska ha radianer till, men det kommer en och annan godbit i taget :-)
När du skall derivera eller integrera trigonometriska funktioner så är det väldigt mycket enklare om man arbetar med radianer.
Ja det ante mig. Har kikat lite på de kommande kapitlen och de ser riktigt lovande ut 😊
Här kommer min egen lösning.
Visa spoiler
Eftersom 2 radier minus ett (två radier räknar sträckan med längd två gånger, så vi får dra bort den en gång) är lika med får vi , d.v.s. .
Man kan sedan dra en sträcka från cirkelsektorernas skärningspunkt vinkelrätt mot triangelns bas. Då uppstår två kongruenta rätvinkliga trianglar. Cosinus och Pythagoras sats ger då följande information:

Sedan kan vi, om vi ger områdena lite färg, inse att två av cirkelsektorerna minus triangeln ger det sökta området.
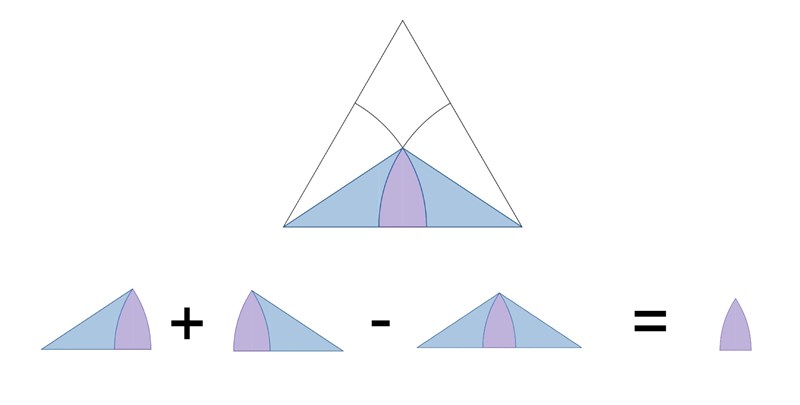
Detta ger oss sedan:
.
AlvinB skrev:Här kommer min egen lösning.
Visa spoiler
Eftersom 2 radier minus ett (två radier räknar sträckan med längd två gånger, så vi får dra bort den en gång) är lika med får vi , d.v.s. .
Man kan sedan dra en sträcka från cirkelsektorernas skärningspunkt vinkelrätt mot triangelns bas. Då uppstår två kongruenta rätvinkliga trianglar. Cosinus och Pythagoras sats ger då följande information:
Sedan kan vi, om vi ger områdena lite färg, inse att två av cirkelsektorerna minus triangeln ger det sökta området.
Detta ger oss sedan:
.
Nice! Mina tankar gick i liknande banor först, inspirerat av inklusion-exklusion i sannolikhetsläran/venndiagram. När jag kom på integralen så körde jag på den istället, men din lösning är exakt vad jag önskar att jag själv hade kommit på. :)
Hej, ett osäkert försök ifrån mej )
Jag tänker mej att radien är skärningspunkten i x-led + sin 30° dvs 2.5+0.5 =3
sen tar jag % skillnaden i x-led mellan skärningspunkten och radien = 2.5/3 = 0.166666667
= 1/6 ,, sen räknar jag ut hela ena sektor arean jag kallar sektor A-arean
enligt formeln Aa = (r^2/2) * ( 60°/ 180-sin60°) =... areaenheter * 1/6
sen tar jag det x(ae)*2 = hela skuggade partiets area ?)
tacksam för guidning av vad jag missat )
....






