cos(60+x)-cos(60+x)= -sqrt3 sin(c)

 Min lösning: $$\begin{gathered} \cos \left(60°+x\right)-\cos \left(60°-x\right)=-\sqrt{3\sin \left(x\right)} \Rightarrow \\ (\cos \left(60\right)\times \cos \left(x\right)-\sin \left(60\right)\times \sin \left(x\right))-(\cos \left(60\right)\times \cos \left(x\right)+\sin \left(60\right)\times \sin \left(x\right))\Rightarrow \leftarrow Använder additions och substraktionssattsen. \\ (\frac{1}{2}\times \cos (x) -\frac{\sqrt{3}}{2}\times \sin (x\left)\right)-(\frac{1}{2}\times \cos (x) + \frac{\sqrt{3}}{2}\times \sin (x\left)\right) \Rightarrow \leftarrow omvandlar till exakta värden. \\ (\frac{1}{}\times \cos (x) -\frac{\sqrt{3}}{}\times \sin (x\left)\right)-(\frac{1}{}\times \cos (x) + \frac{\sqrt{3}}{}\times \sin (x\left)\right) \Rightarrow \leftarrow allt är dividerat med 2, så jag tar bort 2:an \\ \left(\cos \right(x) -\sqrt{3}\sin (x\left)\right)-\left(\cos \right(x) + \sqrt{3}\sin (x\left)\right)\Rightarrow \leftarrow Bytar tecken på + \sqrt{3}\sin \left(x\right) till - \sqrt{3}\sin \left(x\right) för att ta bort parantesen ? \\ \mathbf{-}\sqrt{\mathbf{3}}\mathit{s}\mathit{i}\mathit{n}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{-}\sqrt{\mathbf{3}}\mathit{s}\mathit{i}\mathit{n}\mathit{x}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{2}\mathbf{ }\sqrt{\mathbf{3}}\mathbf{ }\mathit{s}\mathit{i}\mathit{n}\mathbf{(}\mathit{x}\mathbf{)}\mathbf{\Leftarrow }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{h}\mathit{ä}\mathit{r}\mathbf{ }\mathit{t}\mathit{r}\mathit{o}\mathit{r}\mathbf{ }\mathit{j}\mathit{a}\mathit{g}\mathbf{ }\mathit{d}\mathit{e}\mathit{t}\mathbf{ }\mathit{b}\mathit{l}\mathit{i}\mathit{r}\mathbf{ }\mathit{f}\mathit{e}\mathit{l}\mathbf{.}\mathbf{.} \end{gathered}$$

 Facits svar: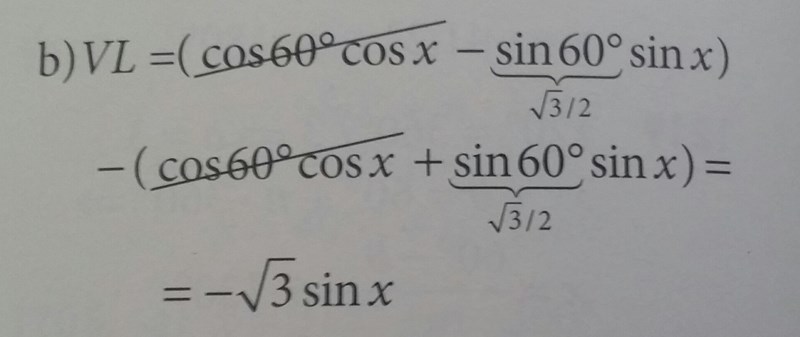 

Det vore bättre om du redigerar ditt förstainlägg i stället för att bumpa din tråd 2 ggr på kort tid.

Du gör fel när du "tar bort 2:an" - det innebär att du multiplicerar allt med 2, så det är inte konstigt att ditt svar är multiplicerat med 2 också.

hhmmm... okej, om jag förstår de rätt blir de : 

$$\begin{gathered} (\frac{1}{2}\times \cos (x) -\frac{\sqrt{3}}{2}\times \sin (x\left)\right)-(\frac{1}{2}\times \cos (x) + \frac{\sqrt{3}}{2}\times \sin (x\left)\right) \Rightarrow . \\ \frac{1}{2}\cos \left(x\right) -\frac{\sqrt{3}}{2}\sin \left(x\right)-\frac{1}{2}\cos \left(x\right) - \frac{\sqrt{3}}{2}\sin \left(x\right)) \Rightarrow \\ -2 \times \frac{\sqrt{3}}{2}\sin (x) \Rightarrow -\frac{\sqrt{3}}{2}\sin (x) \\ \mathbf{.} \end{gathered}$$

:)

Ja, det stämmer, ända tills sista ledet där du tappar bort en tvåa. 2 i täljaren och 2 i nämnaren skall ta ut varandra. Facit har insett lite snabbare än du att de båda termer som de har strukit över tar ut varandra.

ja, det är klart... :P  glömde att ta bort 2:an i nämnaren. Om 2:orna tar ut varandra blir det som facit vill :)

$$\begin{gathered} (\frac{1}{2}\times \cos (x) -\frac{\sqrt{3}}{2}\times \sin (x\left)\right)-(\frac{1}{2}\times \cos (x) + \frac{\sqrt{3}}{2}\times \sin (x\left)\right) \Rightarrow . \\ \frac{1}{2}\cos \left(x\right) -\frac{\sqrt{3}}{2}\sin \left(x\right)-\frac{1}{2}\cos \left(x\right) - \frac{\sqrt{3}}{2}\sin \left(x\right)) \Rightarrow \\ -2 \times \frac{\sqrt{3}}{2}\sin (x) \Rightarrow -\sqrt{3}\sin (x) \end{gathered}$$

Hej!

För att lösa denna uppgift kan du använda mitt inlägg i

Päivis tråd

Du kan skriva

    $\displaystyle \cos(60^\circ + x) - \cos(60^\circ - x) = -2\sin 60^\circ \cdot \sin x.$

Eftersom $\sin 60^\circ = \frac{\sqrt{3}}{2}$ så följer det att

    $\displaystyle -2\sin 60^\circ \cdot \sin x = -\sqrt{3} \cdot \sin x$

och uppgiften är löst.

Albiki