Cos till radianer
Hej min uppgift är skriv cos1.2 i radianer.
Men vad exakt menas med cos1.2?
Liksom hur många grader är det?
I enhetscirkeln blir tal aldrig större än 1 så vet inte hur jag ska tänka kring det.
Läst matte för många år sedan och har glömt vad "cos1.2" menas.
Tack på förhand
Jo, enhetscirkeln har vinklar i radianer från 0 till . Och man kan räkna med hur stora argument som helst till de trigonometriska funktionerna - för allt som är mer än ett varv på enhetscirkeln drar man bort hela varv tills man har något som är mindre än ett varv.
Edit: tillägg: det som aldrig blir större än 1 i enhetscirkeln är x och y.
Men förresten är "skriv cos1.2 i radianer" lite konstigt. 1,2 radianer är vettigt, men resultatet av cos är inte en vinkel. Lyder uppgiften precis så?
skriv cos1.2 i radianer.
Det här är en obegriplig uppgift - du måste ha skrivit av det fel. Kan du ta en bild av uppgiften och lägga in den här?
Tack för svar men jag blir inget klokare, ska jag ta bort 1? och räkna 0.2 som en femtedel av 360 grader? Vilket i så fall är 72 grader och sedan göra om det till radianer?
Vad menas med uttrycket till och börja med?
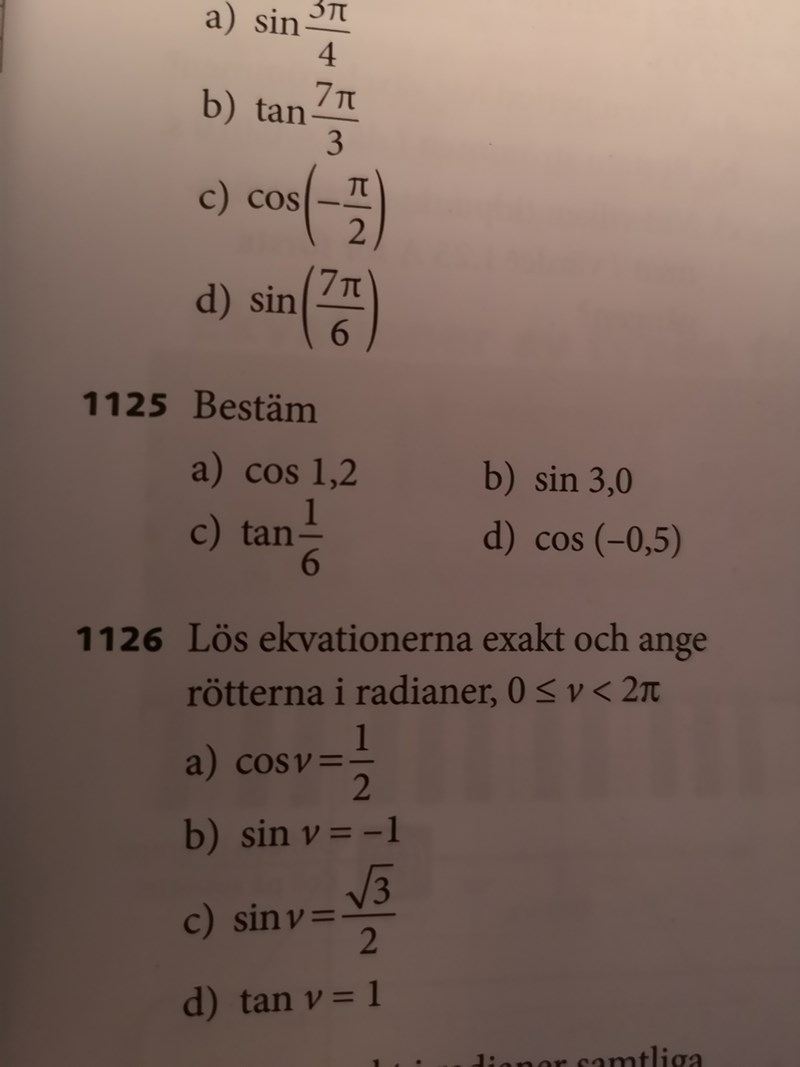
1125A Foto finns här
Ta ett foto av uppgiften och lägg in här. Så som du har skrivit den är den obegriplig. /moderator
Tryck in 1,2 på miniräknaren och sedan cos. Se till att räknaren är inställd på radianer.
@Smaragdalena Foto är uppladdat i mitt senaste inlägg.
Eftersom ett helt varv är radianer som jag sa förut, och 360 grader, så är 1,2 radianer = grader.
@Laguna, ja absolut går det och rätt svar blir det också, men hur räknar man ut det?
Eftersom ett helt varv är 2π radianer som jag sa förut, och 360 grader, så är 1,2 radianer = 1,2×360/(2π)1,2×360/(2π) grader.
Ja absolut här är jag helt med "1,2 radianer = 1,2×360/(2π)1,2×360/(2π) grader."
Men hur blev cos1.2, 0.36 radianer?
Vad exakt menas med COS1.2???
Ska jag tänka att cos1.2 är 432grader?
Eller hur ska jag tänka?
Majken skrev:@Smaragdalena Foto är uppladdat i mitt senaste inlägg.
Det var något helt annat! Så som det står i uppgiften betyder det att du skall räkna ut cosinusvärdet för vinkeln 1,2 radianer. Det gör du med hjälp av din miniräknare. Hur man matar in det är olka på olika miniräknar-modeller - på vissa skall man först skriva in värdet 1,2 och trycka på en knapp märkt "cos", på andra skall man först trycka på knappen "cos" och sedan mata in värdet 1,2. I båda fallen måste du se till att räknaren är inställd på radianer, inte grader.
Om vi skippar miniräknaren, hur räknar man då ut det?
"Eftersom ett helt varv är 2π2π radianer som jag sa förut, och 360 grader, så är 1,2 radianer = 1,2×360/(2π)1,2×360/(2π) grader"
Med denna formel får jag ungefär 20.62grader vilket är 0.36 radianer.
Låter rimligt då en radian är cirka 57.3grader.
Men mitt problem i det hela är hur blir Cos1.2 =20.62grader?
Detta är något jag inte kan se.
Det gör man inte. :)
@Micimacko Dum fråga kanske men vrf inte? Jag vill förstå hela uträkningen.
Majken skrev:Med denna formel får jag ungefär 20.62grader vilket är 0.36 radianer.
Låter rimligt då en radian är cirka 57.3grader.
Men mitt problem i det hela är hur blir Cos1.2 =20.62grader?
Detta är något jag inte kan se.
Det blir det inte.
- Radianer är en enhet som kan användas för att ange vinklar.
- Grader är en annan enhet som också kan användas för att ange vinklar.
På samma sätt som
- Centimeter är en enhet som kan användas för att ange sträckor.
- Tum är en annan enhet som också kan användas för att ange sträckor.
Vi kan omvandla mellan radianer och grader på följande sätt:
2pi radianer är lika med 360 grader.
Det betyder att 1 radian är lika med 360/2pi grader.
Alltså är 1.2 radianer lika med 1.2*360/2pi grader, vilket är ungefär lika med 69 grader.
Alltså är cos(1.2 radianer) ungefär lika med cos(69 grader), vilket i sin tur är ungefär lika med 0.36.
Majken skrev:Om vi skippar miniräknaren, hur räknar man då ut det?
"Eftersom ett helt varv är 2π2π radianer som jag sa förut, och 360 grader, så är 1,2 radianer = 1,2×360/(2π)1,2×360/(2π) grader"
Med denna formel får jag ungefär 20.62grader vilket är 0.36 radianer.
Låter rimligt då en radian är cirka 57.3grader.
Men mitt problem i det hela är hur blir Cos1.2 =20.62grader?
Detta är något jag inte kan se.
Jag förstår inte vad du gör. Varför är de formler jag skrev fördubblade? 1,2 radianer är ett visst antal grader, naturligtvis större än 57, och det är inte mer med det.
Det är fortfarande så att cos1,2 inte blir vare sig radianer eller grader utan bara ett tal.
Majken skrev:@Micimacko Dum fråga kanske men vrf inte? Jag vill förstå hela uträkningen.
Av samma anledning som man inte räknar ut cos 27,3 grader för hand. Det finns inga smidiga sätt att få ett bra svar. Det närmsta du kan komma tror jag är om du ritar en stor triangel med rätt vinkel och delar sidorna med varandra.
Majken skrev:...
Men vad exakt menas med cos1.2?
...
Med cos1.2 menas cos(1.2), dvs cosinusvärdet av vinkeln 1.2 radianer.
Cos är alltså en förkortning av namnet på den trigonometriska funktionen cosinus.
Läs mer om sinus och cosinus här och fråga om det du inte förstår.
Majken skrev:@Micimacko Dum fråga kanske men vrf inte? Jag vill förstå hela uträkningen.
Det finns vissa vinklar för vilka vi känner till de exakta cosinusvärdena, men för de allra flesta vinklarna går dessa värden inte att räkna ut för hand.
Jämför t.ex. uttrycket som vi enkelt kan beräkna värdet av för hand.
Medans uttrycket inte lika lätt går att beräkna utan miniräknare.
Uträkningen ovan vet jag inte vad som gick snett.
Majken skrev:Med denna formel får jag ungefär 20.62grader vilket är 0.36 radianer.
Låter rimligt då en radian är cirka 57.3grader.Men mitt problem i det hela är hur blir Cos1.2 =20.62grader?
Detta är något jag inte kan se.
Gud vad allt blev fel, och kom nyss fram till att (cos69 grader) är samma som det jag aldrig förstod var att en radian är cirka 57.3grader och sedan *1.2 och sedan cos på det.
@Laguna
Tänkte att svaret var 0.36 och tog det baklänges men vet inte vad som blev snett.
@Yngve
som Yngve skrev så är det samma sak vilket jag nyss kom fram till.
Och talen i sinus och cosinus är grader, och det jag får ut är x eller y koordinaten i en enhetscirkel?
Du får ut en siffra, som är lika stor som koordinaten på enhetscirkeln :)
Majken skrev:Uträkningen ovan vet jag inte vad som gick snett.
Majken skrev:Med denna formel får jag ungefär 20.62grader vilket är 0.36 radianer.
Låter rimligt då en radian är cirka 57.3grader.Men mitt problem i det hela är hur blir Cos1.2 =20.62grader?
Detta är något jag inte kan se.
Gud vad allt blev fel, och kom nyss fram till att (cos69 grader) är samma som det jag aldrig förstod var att en radian är cirka 57.3grader och sedan *1.2 och sedan cos på det.
@Laguna
Tänkte att svaret var 0.36 och tog det baklänges men vet inte vad som blev snett.
@Yngve
som Yngve skrev så är det samma sak vilket jag nyss kom fram till.
Och talen i sinus och cosinus är grader, och det jag får ut är x eller y koordinaten i en enhetscirkel?
Om du tar ex. sin( 30 grader) så kommer du få ut ett sinusvärde för 30 grader.
Värdet du får ut anger alltså förhållandet mellan den motstående kateten och hypotenusan vid en vinkel som är 30 grader.
sin 30 har ett exakt värde som är 1/2 eller 0,5. Det betyder alltså att den motstående kateten är hälften så lång som hypotenusan vid 30 graders vinkel
Om du tar ex. cos(78 grader) så kommer du få ett cosinusvärde för 78 grader
Eftersom
så berättar cosinusvärdet förhållandet mellan närliggande kateten och hypotenusan vid 78 graders vinkel.
cos(78 grader)=Inget exakt värde men det berättar att den motstående kateten är ungefär en femtedel av hypotenusans längd.
tan(45 grader) ger tangensvärdet för en vinkel som är 45 grader
Eftersom
så berättar tangensvärdet förållandet mellan de båda kateterna. tan(45 grader)=1. Detta betyder att vid en 45 graders vinkel är de båda kateterna lika långa.
Detta kanske också hjälper till att förstå varför vissa värden är exakta och andra värden inte är exakta. Ibland är fårhållandet exakt och ibland inte.
Denna bild kanske också hjälper att förstå sinusvärdet
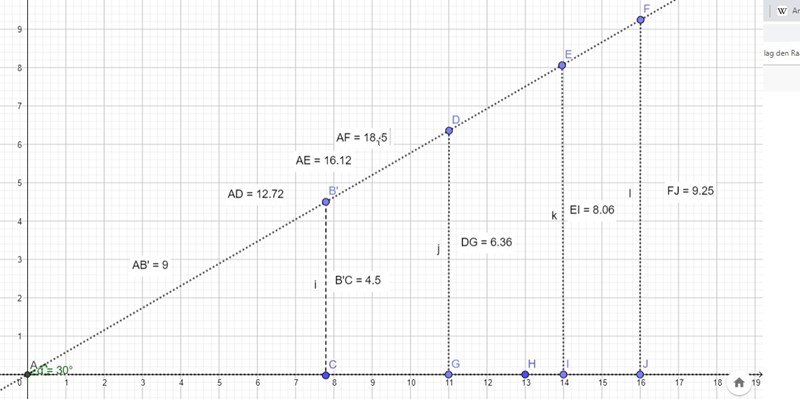
Här har jag nere vid A skapat en vinkel som är 30 grader som skapats av två streckade vinkelben som fortsätter utåt. Sedan kan jag bilda som du ser olika stora rätvinkliga trianglar. Du kan se att det finns en rätvinklig triangel ABC, en rätvinklig triangel ADG, en rätvinklig triangel AEI och så vidare. Dessa har olika långa kateter och hypotenusan. Men om du tittar på mina mätningar av sträckorna så kan du se att den motstående kateten till 30 graders vinkeln ALLTID är hälften så liten som hypotenusan. Därför vet vi att sin(30 grader)=0,5
Titta på bilden här nedan. Här har jag ritat upp en vinkel som är 78 grader.
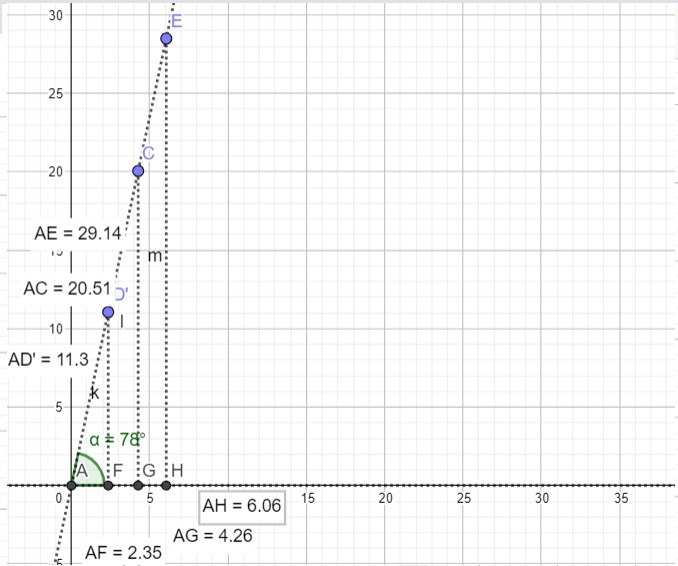
Här vill jag studera cosniusvärdet för en 78 graders vinkel alltså cos(78 grader). Detta som är förhållandet mellan den närliggande kateten och hypotenusan för en 78 graders vinkel. Här har jag också bildat olika stora rätvinkliga triangllar. Triangel ADF, Triangel AGC, Traingel AEH. Här kan jag dock inte hitta ett enkelt samband mellan närliggande kateten och hypotenusan. I första triangeln är den närliggande 2,35 och hypotenusan 11,3. I nästa är den närliggande 4,26 och hypotenusan 20,51. Då kan jag kanske gissa mig till att den närliggande är ungefär en femtedel av hypotenusan och att förhållandet då är ca. 0,2. Jag kan dock testa att slå förhållandet på en räknare ex.
Detta är samma sak som vi får om vi slår cos(78) då räknaren ger ett värde med massor av decimaler som är ca. 0,2079116908
Majken skrev:
Gud vad allt blev fel, och kom nyss fram till att (cos69 grader) är samma som
Nej så får du inte skriva. Ett likhetstecken innebär ett påstående. Det du alltså påstår är att , vilket inte stämmer. Det du antagligen menar är att cosinus av det som står till vänster är (ungefär) lika med 0.36.
Det du alltså ska skriva är
Och talen i sinus och cosinus är grader, och det jag får ut är x eller y koordinaten i en enhetscirkel?
Vinkeln som ges i t.ex. cosinus kan antingen vara angiven i grader eller i radianer.
Men det är olika cosinusfunktioner som används beroende på hur vinkeln anges.
Dvs cos(23) och cos(23) ger olika resultat, beroende på om vinkeln 23 anges i grader eller radianer.
Du väljer vilken av cosinusfunktionerna som används genom en inställning på räknaren (deg/rad eller liknande).
---------
Egentligen finns det bara en cosinusfunktion, den där vinkeln anges i radianer, men genom att du ställer in "deg" på räknaren så gör den automatiskt nödvändiga omvandlingar mellan grader och radianer.
Problemet är att det kanske inte alltid är självklart vilken enhet som använts för att ange vinklar om det inte tydligt anges.
I dessa fall kan du använda följande tips:
- Från och med Matte 4 så är det "alltid" radianer som avses.
- Om vinkeln innehåller så är den antagligen angiven i radianer. Ex .
- Om vinkeln är en jämn multipel av 15 så är den troligtvis angiven i grader. Ex 15, 30, 45, 60, 75, 90 o.s.v.
Om det inte är självklart eller tydligt framgår vilken enhet som används/ska användas så kan du alltid skriva en kommentar i din lösning typ:
"Jag förutsätter här att vinklarna anges i radianer"
Tillägg till Yngves tips: Om det står t ex 54o så är det vinkeln 54 grader.
Ännu ett tillägg:
Det finns en konvention (dvs ett sätt man brukar göra på) som går ut på att man inte skriver ut enheten radianer. Dvs jobbar man med grader så skriver man en symbol - tex sin(57°), men jobbar man med radianer skriven man inget - tex sin(0,9).
Jag tycker den här tråden är ett exempel på varför det är en dålig konvention som ofta leder till missförstånd! Det vore bättre om man skrev sin(0,9 rad), eller använde en annan symbol.
Hej alla, och tack för samtliga svar.
Har gått över lite Matte 1 uppgifter och nu känns det som jag är mer med i matchen.
Om du tar ex. sin( 30 grader) så kommer du få ut ett sinusvärde för 30 grader.
sin (v)=motstående katethypotenusasin (v)=motstående katethypotenusa
Värdet du får ut anger alltså förhållandet mellan den motstående kateten och hypotenusan vid en vinkel som är 30 grader.
sin 30 har ett exakt värde som är 1/2 eller 0,5. Det betyder alltså att den motstående kateten är hälften så lång som hypotenusan vid 30 graders vinkel
Om du tar ex. cos(78 grader) så kommer du få ett cosinusvärde för 78 grader
Eftersom cos v=närliggande katethypotenusancos v=närliggande katethypotenusan
så berättar cosinusvärdet förhållandet mellan närliggande kateten och hypotenusan vid 78 graders vinkel.
cos(78 grader)=0,207911...0,207911...Inget exakt värde men det berättar att den motstående kateten är ungefär en femtedel av hypotenusans längd.
tan(45 grader) ger tangensvärdet för en vinkel som är 45 grader
Eftersom tan(v)=motstående katetnärliggande katettan(v)=motstående katetnärliggande katet
så berättar tangensvärdet förållandet mellan de båda kateterna. tan(45 grader)=1. Detta betyder att vid en 45 graders vinkel är de båda kateterna lika långa.
Räknade lite med sinus och cosinus samt Pytagoras sats .
Och har fått bättre förståelse för hur sinus och cosinus funkar.
Tex
Men hur lång är den närstående kateten tänkte jag?
Några problem som jag har haft med sinus och cosinus löste sig där.
Och min förståelse har ökat då sin eller cos aldrig kan bli större än 1 i relations till hypotenusan.
Nej så får du inte skriva. Ett likhetstecken innebär ett påstående. Det du alltså påstår är att 1.2⋅180π=0.361.2·180π=0.36, vilket inte stämmer. Det du antagligen menar är att cosinus av det som står till vänster är (ungefär) lika med 0.36.
Det du alltså ska skriva är cos(1.2⋅180π)≈0.36
Ja det stämmer då det är ungefär 0.36, slarvmisstag där.
Ännu ett tillägg:
Det finns en konvention (dvs ett sätt man brukar göra på) som går ut på att man inte skriver ut enheten radianer. Dvs jobbar man med grader så skriver man en symbol - tex sin(57°), men jobbar man med radianer skriven man inget - tex sin(0,9).
Jag tycker den här tråden är ett exempel på varför det är en dålig konvention som ofta leder till missförstånd! Det vore bättre om man skrev sin(0,9 rad), eller använde en annan symbol.
Tack för tipset! Ska verkligen hålla koll på vilken enhet de frågar efter!.
Liten slutfråga men om sinus är 1 alltså 90 grader ska man tänka "triangeln som ett rakt streck?"
Majken skrev:
Liten slutfråga men om sinus är 1 alltså 90 grader ska man tänka "triangeln som ett rakt streck?"
Bra fråga!
Svar: Nej.
Sambandet mellan sinusvärdet och kvoten "motstående katet"/"hypotenusa" gäller endast för de spetsiga vinklarna i rätvinkliga trianglar.
Och en vinkel som är 90° är inte spetsig, så där gäller inte sambandet.
Sinus och cosinus för godtyckliga vinklar kan istället definieras med hjälp av enhetscirkeln.






