Definitionsfråga växande/avtagande
Hej! Är riktigt förvirrad och uppskattar hjälp inför mitt prov i morgon.
När använder man inkluderande intervall för att beskriva att en graf är växande/avtagande/strikt växande/strikt avtagande?
Jag tycker min bok gör fel. Se denna fråga t.ex.
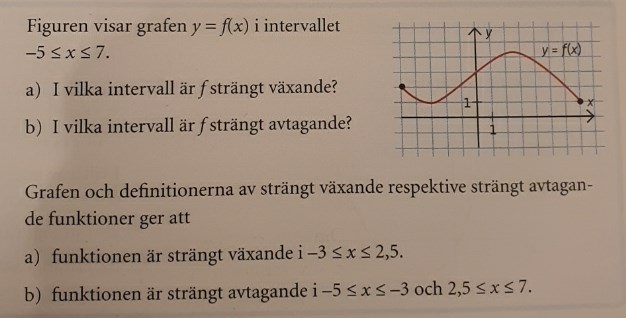
Här kallar man det för strängt växande fastän derivatan är 0 i ändarna av intervallet. Se a) t.ex. Där har man inkluderat -3 och 2,5 inom intervallet. Jag hade själv skrivit -3 < x < 2,5 i stället. Det de har gjort i boken skulle bara vara rätt enligt mig om uppgiften frågande om allmänt växande, d.v.s. inte strikt växande. Tänker jag rätt?
Kan någon bekräfta detta? Det här är min definition:
Om intervallet inkluderar en punkt med derivatan 0, men intervallet i övrigt är växande, så är intervallet växande.
Om intervallet utesluter punkter med derivatan 0 (genom att sätta mer än-tecken eller mindre än-tecken), och bara är växande, så är intervallet strikt växande.
Och vice versa när det gäller avtagande respektive strikt avtagande.
Tack!!!!!
En funktion är strängt växande då
f(b) > f(a)
om
b > a.
Derivatan kan vara 0 i enstaka punkter för en strängt växande funktion. Ett klassiskt exempel är
f(x) = x^3
som är strängt växande överallt, trots att f'(0) = 0.
Komplettering:
En funktion är växande då
om
Derivatan kan vara 0 överallt för en växande funktion. Ett klassiskt exempel är
som är växande överallt, trots att .
Definitionen gäller även för avtagande funktioner om du byter ut mot .
Detta leder till den icke-intuitiva slutsatsen att en funktion kan vara både växande och avtagande överallt.
Läs gärna mer detta i avsnittet om monotona funktioner.
Nej, dina definitioner är fel. Det är tillåtet för en strängt växande funktion att ha derivatan 0 i en punkt (eller flera punkter) men inte i ett intervall.
Funktionen y=5 år både växande och avtagande, men varken strängt växande eller strängt avtagande. Funktionen y = x3 är strängt växande för alla reella tal, fastän derivatan är 0 i en punkt.
Tack för svaren.
Men hur vet jag om jag ska använda < och > eller ≤ och ≥ för att definiera intervallet?
Det är tillåtet för en strängt växande funktion att ha derivatan 0 i en punkt (eller flera punkter) men inte i ett intervall.
Men en graf som går sicksack och halva tiden har derivatan 0 och halva tiden derivatan > 0 är väl inte strängt växande?
Om ändpunkten ska ingå i intervallet så ska du använda (resp. ), annars ska du använda (resp. ).
Så frågan är då om ändpunkterna ingår i det intervall för vilket funktionen är strängt växande (strängt avtagande).
Vad tycker du själv om den frågan?
Gäller definitionerna vi har givit dig om a eller b är lika med -3 respektive 2,5?
========
En funktion kan vara (strängt) växande i vissa intervall och (strängt) avtagande i andra intervall.
Ta r.ex.
Den funktionen är strängt avtagande för alla och strängt växande för alla .
Zeus skrev:Tack för svaren.
Men hur vet jag om jag ska använda < och > eller ≤ och ≥ för att definiera intervallet?
Det är tillåtet för en strängt växande funktion att ha derivatan 0 i en punkt (eller flera punkter) men inte i ett intervall.
Men en graf som går sicksack och halva tiden har derivatan 0 och halva tiden derivatan > 0 är väl inte strängt växande?
Om en derivata är 0 i mer än en punkt så är funktionen inte strängt växande, bara växande.
Smaragdalena skrev:
Om en derivata är 0 i mer än en punkt så är funktionen inte strängt växande, bara växande.
Om du menar att derivatan är lika med 0 överallt i ett intervall så stämmer det du skriver, annars inte.
Vi kan till exempel ha en funktion som är strängt växande överallt trots att den har två olika terrasspunkter.
Ok, så jag har förstått nu att jag bör använda inkluderande intervall d.v.s. >= och =<. Jag förstår syftet med detta då derivata på 0 också räknas som växande/avtagande.
Men se följande uppgift. Här använder facit bara < och > Varför?
Pluggakuten spökar för mig så jag lyckas inte infoga någon bild på uppgiften. Bilden är på en linjär graf y = f´(x) och utifrån denna graf ska man bestämma vilket intervall som funktionen f är strängt växande.
Facit säger x > 3 men jag tycker det ska vara x >= 3
Det är tyvärr omöjligt att ge ett bra svar på din fråga utn att se bilden.
Pröva att ta bilden med lägre upplösning så att den inte blir så stor.
Yngve skrev:Det är tyvärr omöjligt att ge ett bra svar på din fråga utn att se bilden.
Pröva att ta bilden med lägre upplösning så att den inte blir så stor.


Nu verkar det fungera. I facit används bara < och > för att svara på dessa frågor.
Vad gäller 4104 håller med dug.
Det ser ut som att , vilket innebär att , där är en konstant.
Denna funktion är strängt växande då och strängt avtagande då .
Gör gärna en ny tråd för de andra frågorna och visa där hur du resonerar.
Yngve skrev:Vad gäller 4104 håller med dug.
Det ser ut som att , vilket innebär att , där är en konstant.
Denna funktion är strängt växande då och strängt avtagande då .
Gör gärna en ny tråd för de andra frågorna och visa där hur du resonerar.
Men vad är skillnaden? Jag vill ju gärna förstå varför dessa två uppgifter räknas ut på olika sätt, vad är skillnaden som gör att de inte räknas likadant?
För att kunna lösa uppgifterna behöver vi veta hur de efterfrågade funktionerna uppför sig.
I den ena uppgiften har vi en graf av en funktion f(x) att utgå från, i den andra uppgiften har vi en graf av en derivatafunktion f'(x) att utgå från.
Därför skiljer sig tillvägagångssättet i lösningarna av de två uppgifterna.
Men den viktiga frågan är om du förstår resonemanget i de båda lösningarna?
Yngve skrev:För att kunna lösa uppgifterna behöver vi veta hur de efterfrågade funktionerna uppför sig.
I den ena uppgiften har vi en graf av en funktion f(x) att utgå från, i den andra uppgiften har vi en graf av en derivatafunktion f'(x) att utgå från.
Därför skiljer sig tillvägagångssättet i lösningarna av de två uppgifterna.
Men den viktiga frågan är om du förstår resonemanget i de båda lösningarna?
Tyvärr förstår ej alls och får lite smått panik. Båda uppgifter frågar ju om huruvida en funktion f(x) växer. Som hjälpmedel använder man derivata. Jag ser ingen skillnad.
Zeus skrev:
Tyvärr förstår ej alls och får lite smått panik. Båda uppgifter frågar ju om huruvida en funktion f(x) växer. Som hjälpmedel använder man derivata. Jag ser ingen skillnad.
Nej, derivatan används inte som hjälpmedel i lösningen av den första uppgiften, där används istället endast utseendet hos grafen till f(x).
I den andra uppgiften vet vi inte hur grafen till funktionen f(x) ser ut, där vet vi endast hur grafen till derivatafunktionen ser ut.
Yngve skrev:Zeus skrev:Tyvärr förstår ej alls och får lite smått panik. Båda uppgifter frågar ju om huruvida en funktion f(x) växer. Som hjälpmedel använder man derivata. Jag ser ingen skillnad.
Nej, derivatan används inte som hjälpmedel i lösningen av den första uppgiften, där används istället endast utseendet hos grafen till f(x).
I den andra uppgiften vet vi inte hur grafen till funktionen f(x) ser ut, där vet vi endast hur grafen till derivatafunktionen ser ut.
Men den första uppgiften har grafen f'(x), inte f(x)
Då pratar vi om olika saker.
Jag menar att den första uppgiften var den du startade tråden med, här.
Och att den andra uppgiften var 4104.
Vilka menar du?
Yngve skrev:Då pratar vi om olika saker.
Jag menar att den första uppgiften var den du startade tråden med, här.
Och att den andra uppgiften var 4104.
Vilka menar du?
Jag trodde du menade de två som jag lade ut i samma inlägg.
Strunt samma, nu blev det lite tydligare. Nästan framme. Behöver bara förstå varför det är så här som du beskriver:
Nej, derivatan används inte som hjälpmedel i lösningen av den första uppgiften, där används istället endast utseendet hos grafen till f(x).
I den andra uppgiften vet vi inte hur grafen till funktionen f(x) ser ut, där vet vi endast hur grafen till derivatafunktionen ser ut.
Okej, så jag ser skillnaden. Men rent praktiskt vad är nyttan med att skilja på dessa två fall? Jag kan ju rita en graf f'(x) utifrån en graf f(x), och vice versa. Varför ska man skilja på dem om man kan gå från den ena till den andra när man vill?
Tack och sorry om det blev förvirrande förut.
Jag förstår inte vad du menar med frågan om nyttan att skilja på de två fallen.
Om uppgifterna är formulerade på olika sätt så är det naturligt att lösningsmetoderna är olika.
=============
Ja, du kan rita en graf till f'(x) om du vet hur grafen till f(x) ser ut.
Men nej, du kan inte rita en graf till f(x) om du endast vet hur f'(x) ser ut.
Exempel:
Om så vet du att .
Men om så vet du bara att , där är en okänd konstant. Du vet alltså inte hur grafen till ser ut.
Man behöver hålla reda på vilken som är vilken om man inte skall råka göra allting baklänges utan att det var meningen.
Du kan rita en graf för f'(x) om du vet hur f(x) ser ut, som i bilden i början, men om du inte vet formeln för f(x) så måste du göra massor med mätningar i grafen. Frågan gällde bara var f(x) var växande och det kan du avläsa direkt i grafen, utan att gå via derivatan.
Om man bara har f'(x) så kan man göra motsvarande. Man kan mäta i grafen och rita en graf för f(x) (efter att ha bestämt sig var den ska gå i höjdled, eftersom f(x)+C och f(x) har samma derivata, som Yngve påpekar). Men här är det likadant som ovan, du kan se direkt i grafen för f'(x) när f(x) är växande.
Yngve skrev:Jag förstår inte vad du menar med frågan om nyttan att skilja på de två fallen.
Om uppgifterna är formulerade på olika sätt så är det naturligt att lösningsmetoderna är olika.
=============
Ja, du kan rita en graf till f'(x) om du vet hur grafen till f(x) ser ut.
Men nej, du kan inte rita en graf till f(x) om du endast vet hur f'(x) ser ut.
Exempel:
Om så vet du att .
Men om så vet du bara att , där är en okänd konstant. Du vet alltså inte hur grafen till ser ut.
Tack för tålamodet. Jag förstår skillnaden med konstanter, men det påverkar ju bara y-värdet. När vi definerar ett intervall är det bara x-värdet som är relevant. Så jag kan inte förstå fortfarande. Visst, två olika frågor, två olika lösningsmetoder, men jag tycker de bör ge samma svar i slutändan.
Jag vill inte vara jobbig, men förstår bara ej.
Laguna skrev:Du kan rita en graf för f'(x) om du vet hur f(x) ser ut, som i bilden i början, men om du inte vet formeln för f(x) så måste du göra massor med mätningar i grafen. Frågan gällde bara var f(x) var växande och det kan du avläsa direkt i grafen, utan att gå via derivatan.
Om man bara har f'(x) så kan man göra motsvarande. Man kan mäta i grafen och rita en graf för f(x) (efter att ha bestämt sig var den ska gå i höjdled, eftersom f(x)+C och f(x) har samma derivata, som Yngve påpekar). Men här är det likadant som ovan, du kan se direkt i grafen för f'(x) när f(x) är växande.
Ok säg att vi har en extrempunkt vid x = 3 på en funktion, och efter extrempunkten är derivatan alltid positiv.
Derivatan i extrempunkten är ju 0. Jag ser det med ögonen, lutningen är 0! Så när jag kollar grafen f(x) skriver jag att den är strängt växande då x >= 3 d.v.s. jag inkluderar även x:et för extrempunkten
Nu tittar jag på f'(x) i stället. Här ser jag att grafen skjuter upp genom x-axeln vid vid x = 3 (eftersom derivatan är 0 där). Så jag svarar samma, att f(x) är strängt växande då x >= 3
Zeus skrev:
Tack för tålamodet. Jag förstår skillnaden med konstanter, men det påverkar ju bara y-värdet. När vi definerar ett intervall är det bara x-värdet som är relevant. Så jag kan inte förstå fortfarande. Visst, två olika frågor, två olika lösningsmetoder, men jag tycker de bör ge samma svar i slutändan.
Jag vill inte vara jobbig, men förstår bara ej.
Nej, jag förstår tyvärr inte vad du menar med att de bör ge samma svar.
Det är olika uppgifter. De har olika svar.
Zeus skrev:
Ok säg att vi har en extrempunkt vid x = 3 på en funktion, och efter extrempunkten är derivatan alltid positiv.
Derivatan i extrempunkten är ju 0. Jag ser det med ögonen, lutningen är 0! Så när jag kollar grafen f(x) skriver jag att den är strängt växande då x >= 3 d.v.s. jag inkluderar även x:et för extrempunkten
Nu tittar jag på f'(x) i stället. Här ser jag att grafen skjuter upp genom x-axeln vid vid x = 3 (eftersom derivatan är 0 där). Så jag svarar samma, att f(x) är strängt växande då x >= 3
Ja det stämmer.






