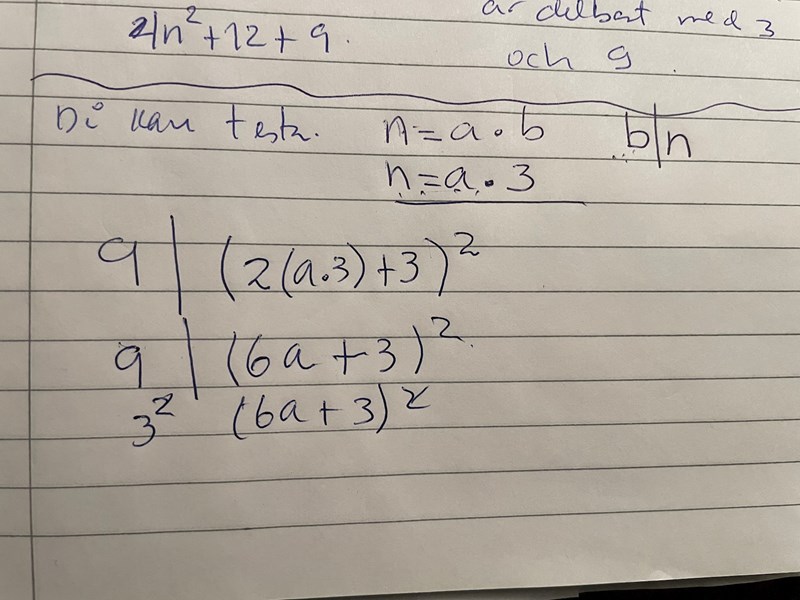Delbarhet

(Vilken ful typsättning i boken.)

3 | n innebär att det finns ett heltal k sådant att n = 3k.

Stämmer det ?

Jag förstår inte tankegången.

Sätt in n = 3k i (2n+3)² och se om det går att dela med 9.

Vad står k för ? Heltal dvs n=ab ? dvs a !

jag tänker att 3 är delbar med 9

då istället för 9 blir det 3^2 

och skriver istället 3^2 | (2n+3)^2

$k$ kan vara vilket heltal som helst. Strategin går ut på att låta $\displaystyle n=3k, k\in\mathbb{Z}$, då vi vet att $3$ delar $n$. Om du stoppar in $3k$ istället för $n$ i uttrycket $(2n+3)^2$, vad händer då?

Ja, men du måste nog förklara lite mer. Hur tänker du exakt? Det är smart att skriva om 9 till 3² som du har gjort, men du måste förklara varför och vad du visar då.

Tips: 6a+3 har ”en trea i sig”, dvs. kan skrivas 3(2a+1). Hur många treor har uttrycket i sig om du kvadrerar?

Tycker att det är lite svårare att kvadrera 3(2a+1)

skulle det bli skillnad med att kvadrera (6a+3) ?

jag tänker på vilka bevis används vi i denna utöver n=ab ?

Vitsen med att kvadrera 3(2a+1) är att man då ser att kvadraten 3²(2a+1)² innehåller faktorn 9, medan det är svårare att se om man kvadrerar 6a+3. Det finns ingen anledning att räkna ut kvadraten mer än så.

Ok. Då förstår jag

hade kvadrera 

(6a+3) 

36a^2+36a+9

9(4a^2+4a+1) innehåller faktor 9 bara 1 gång 

Nu är jag vilse igen

Jag ser inte många 9 nu ? 

Jag förstår inte vad det är du gör.

Visa att om n är ett tal delbart med 3, så är (2n+3)² delbart med 9

Talet n är delbart med 3, så det kan skrivas som 3a. Då är 2n+3 = 2^.3k+3 = 3(2k+1) så (2n+3)² = (3(2k+1))² = 3²(2k+1)² = 9(2k+1)² som är delbart med 9. Klart.

Diskret matematik kurs tredje vecka känns svårt att veta vad ska men göra 

Jag  gjorde kvadreringsregel 

3^2 (2a+1)^2 för att ta bort parenteser 

så vet inte precis vad ska göra i sin helhet

skulle uppskatta lite tips om hur ska jag tänka de många bevis som vi får och svårt att veta när och hur ska användas

spm tex att ersätta n= 3a

Varför skall du räkna ut kvadraten? Det finns ingen anledning.

Du har fått ett fullständigt bevis (men inte på "ren matematiska") i mitt inlägg #15.

Känner mig bara dum att inte förstår. 
kanske blandade med ekvationen lösning där utgår för att använda kvadreringsregel

Har inte öva nästan ingenting med bevis , därför har svårt att hitta tråder

i denna uppgift syftar till att bevisa att 9|(2n+3)^2

och då får jag hjälp av 3|n 

utifrån påståenden heltal b delar heltal n om

det finns en heltal a då skriver n=ab då skriver vi

b|n

men a är inte blir lika med noll 

i uppgiften tänker jag att 3|n att 3 är en del av 9 då menar jag att 9 kan delas i 3^2

därför skrev 3^2 sen fattade inte ordentligt 

varför n=3a men utgår för att det är pga hur många 3 finns i 9 

när jag ersatt n=3a 

i 9|(2(3a)+3)
då frågan är hur ska tänka precis där för att jag ser ingenting och därför löste jag algebraisk 

förstår ni min resonemang?

förstår ni min resonemang?

Nej. Här är ett fullständigt bevis (igen): Är det något steg som är oklart?

Uppgift: Visa att om n är ett tal delbart med 3, så är (2n+3)² delbart med 9

Lösning: Talet n är delbart med 3, så det kan skrivas som 3k.

Då är 2n+3 = 2^.3k+3 = 3(2k+1)

så (2n+3)² = (3(2k+1))² = 3²(2k+1)² = 9(2k+1)² som är delbart med 9.

Klart.

Ok. Tack så mycket 

Lite mer tydligt 

tack så mycket 

Jag märkte att jag hade börjat med att skriva a och sedan bytt det till k, annars ändrade jag ingenting utom att jag la till radbrytningar.

Fick svar  från lärare 

Ska använda k dvs n=3k

sen förstår inte vad  han menar med 9 a ??

Bryt ut en 9a (en nia) är samma sak som bryt ut faktorn nio.

Tack 

vad menas med att utveckla kvadraten ? 
3(2k+) upphöjd till 2 ?

måste lära ut mig förstår dessa uttryck 👍🏽

Att utveckla en kvadrat betyder att gå från (a+b)² till a²+2ab+b².

Ja 

då innebär att jag måste kvadrera 

3^2 ( 2k+1)^2 i uppgiften 

9+ 2.3(2k+1)+ (2k+1)^2 

Nej, jag skrev att du INTE skall utveckla kvadraten, det krånglar bara till det i onödan.

Jag vet att har gjort som du förklarade 

men varför skriver lärare att ska utvecklas kvadrat en.  Sen bryt ut 9a eftersom jag har använt a istället för k 

blir bara mer förvirrad nu