Derivatan av potensfunktioner med bråk i exponenten
Låt säga att vi har följande funktion:
Med deriveringsregeln kan derivatans funktion beräknas:
Men hur kommer man fram till det resultatet ifall man vill använda sig av derivatans definition? Jag har provat använda en central differenskvot men kör fast när jag blir lämnad med i exponenten.
Såhär har jag gjort:
Exponenterna kan skrivas om som enligt .
Här kommer jag inte längre, hur förenklar jag en andragradsfunktion med ett bråk i exponenten? Har provat använda en ekvationsräknare utan succé.
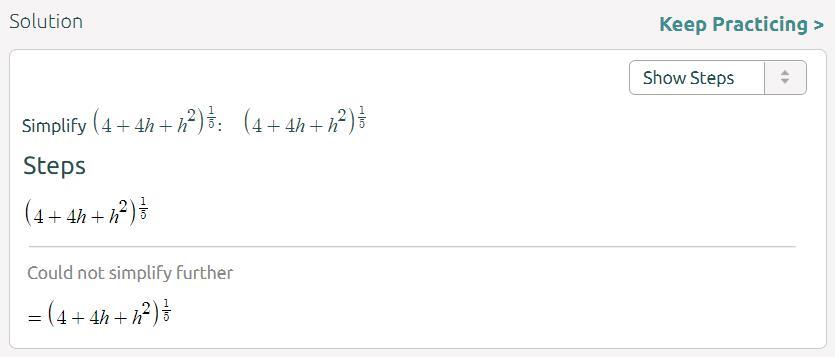
Jag har inget bra svar, men jag sökte efter motsvarande för kubikroten, och fick träffar med "Derivative of Cube Root Function using Definition". Jag har inte riktigt försökt förstå vad han gör. Det kanske går att generalisera till andra rötter.
Det är inte tänkt att du ska kunna lösa dessa med derivatans def.
Men man kan använda här att för att skriva om bråket och sedan låta h gå mot 0.
Som du ser är det oerhört onödigt att pilla med derivatans definition. Är detta en uppgift du håller på med eller bara nyfikenhet?
Dracaena skrev:Som du ser är det oerhört onödigt att pilla med derivatans definition. Är detta en uppgift du håller på med eller bara nyfikenhet?
Bara ren nyfikenhet! Efter att ha suttit och skrivit ut allt för hand de senaste två timmarna har jag dock svurit en ed om att aldrig göra om detta :)
Jag ser varför man aldrig skulle använda detta rent praktiskt, det vara snarare så att jag funderade på hur man gör i en sån situation. Så stort tack för hjälpen, kändes som jag lärde mig en del på det här. I framtiden tänker jag också sno ditt skrivsätt, i mina beräkningar skrev jag ut värdet för a och b redan i första steget. Ser bara lite plottrigt ut... Dessutom blev svaret fel :)

Laguna skrev:Jag har inget bra svar, men jag sökte efter motsvarande för kubikroten, och fick träffar med "Derivative of Cube Root Function using Definition".
Tack ändå för svaret, kändes som det puttade mig i rätt riktning. Jag gjorde samma sökning som dig och fick upp en video som förklarade lösningen för kubikrötter. Ser ut som principen är likadan för alla rötter men att det blir mer invecklat ju större grad roten är av.




