Diff.ekvation - varför kan det ena fallet uteslutas?
Halloj!
På en tentamen jag skrev för ett tag sedan så skulle man lösa följande differentialekvation:
Jag kom efter ett antal korrekta steg fram till:
Här drog jag slutsatsen att lösningen måste innehålla två fall, ett fall där , och ett fall där . Mer specifikt påstår jag att:
Detta var tydligen felaktigt, och jag fattar inte varför det blir fel. Min rättare skrev bara "Du får bara ett fall", och det ger mig inte så mycket insikt i var det har blivit fel.
Du menar väl första ordningens ekvation, d.v.s. , eller?
Man bör nog ta hänsyn till begynnelsevillkoret.
Man är intresserad av den lösning som uppfyller att , d.v.s. den lösning där . Det är alltså bara fallet som är relevant i denna situation.
Om man inte hade något begynnelsevillkor, så får man tre fall som dock kan skrivas ihop m.h.a. en lämpligt vald konstant.
Fall 1 () motsvarar , där är en godtycklig positiv konstant.
Fall 2 () motsvarar den konstanta lösningen , där .
Fall 3 () motsvarar , där är en godtycklig negativ konstant.
Alla tre fall ihopskrivna: , där är ett godtyckligt tal.
Men är inte funktionen jag har definierat i mitt sista stycke också en lösning på differentialekvationen? Om vi stoppar in begynnelsevillkoret bestäms . Således har vi:
Är inte detta en funktion som:
- Satisfierar
- Uppfyller begynnelsevillkoret
?
Tillägg: 10 apr 2025 16:06
Ja, jag menar första ordningen. Skrev fel.
Nej, funktioner och är två separata lösningskurvor som aldrig möts. (De har samma gränsvärde då , men de är aldrig lika)
Lägg märke till att falluppdelning inte gäller den oberoende variabeln , utan funktionskurvans -värde.
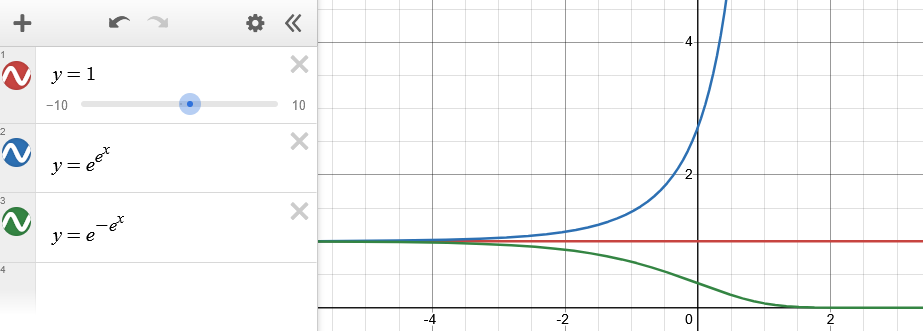
Ah, jag tror jag förstår nu. Det jag har definierat är väl formellt sett inte ens en funktion eftersom varje värde på mappas till två värden på ?
Exakt.
Jag är däremot fortfarande inte riktigt med på hur man ska hantera absolutbeloppet. Hur kan vi veta från början att lösningen ?
Jag antar att du löste ekvationen som en separabel DE.
Vid separationen vill man dividera med uttrycket . Detta uttryck är lika med noll när . Det innebär att divisionen är olagligt ifall . Därmed får man en konstant lösning för alla .
Den givna ekvationen uppfyller (lokalt) förutsättningarna av Picard–Lindelöfs sats om entydigheten av lösningar till ODE:er. Det innebär att det till varje utvald punkt i -planet finns exakt en lösningskurva som går igenom den punkten.
Har man nu någon lösning annan än konstant , så kan den lösningen aldrig korsa linjen eftersom det skulle strida mot entydigheten av ODE:s lösningar. Det finns ju redan lösningen som går igenom alla punkter på linjen .
Man vet alltså att ingen lösningskurva kommer att överskrida den vågräta linjen , så den måste hålla sig antingen under den linjen för alla , eller över den linjen för alla .


