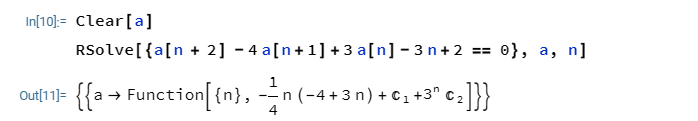Differensekvation - är min lösning ekvivalent med Wolframs?
Halloj!
Jag satt med differensekvationen och försökte lösa denna genom att lösa dess karaktäristiska polynom och genom att försöka ansätta en partikulärlösning och jämföra koefficienter.
Då den KE löses erhålls och . Således vet vi att , där .
Nu kommer vi till den partikulära lösningen. Eftersom en av rötterna är vet jag att vi inte kommer kunna gissa på det typiska . Således testade jag att gissa på , dvs. jag använde "standardtricket" att gångra allting med . Då fick jag efter att ha jämfört koefficienter:
Så den fullständiga lösningen blir:
När jag slår ekvationen på Wolframalpha, däremot, föreslår den:

De får alltså med en åttondel i varje lösning. Min fråga är nu om våra lösningar är ekvivalenta. I min lösning är väl åttondelen helt enkelt inbakad i konstanten ?
Mystiskt, vet inte varifrån 1/8 kommer. Men ja, eftersom A och B eller c1 och c2 är godtyckliga konstanter så är din och wolframs lösningsmängder identiska.
Okej, tack!
Jag har även en fråga om min metod här. Jag har helt enkelt lärt mig genom att lösa en del uppgifter att om man får en rot som är ett kommer den vanliga gissningen inte fungera. Men varför är det så egentligen? Vad hade hänt om vi t.ex. fick en dubbelrot ? Hade vi behövt multiplicera gissningen med istället?
Detta får mig verkligen att undra vilka skillnader som finns mellan wolfram och mathematica då de är gjorda av samma företag. Mathematica returnerar inte konstanten 1/8